Prove that rigorously, and give a combinatorial interpretation. Proceeding from (4.1), show that all combinations (n k)
Question:
Prove that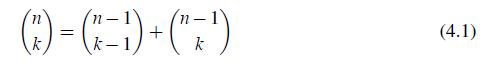
rigorously, and give a combinatorial interpretation. Proceeding from (4.1), show that all combinations (n k) can be arranged in the triangle below, which is constructed in the following way. We start with one in the first row as is shown below, and then, moving down, add two adjacent numbers and write the sum directly underneath. (An empty position is treated as zero.) In other words, each number in the Pascal’s triangle is the sum of the two numbers above it. It helps counting combinations.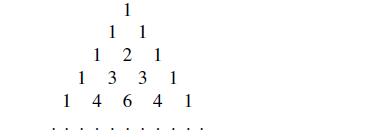
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





