


1.
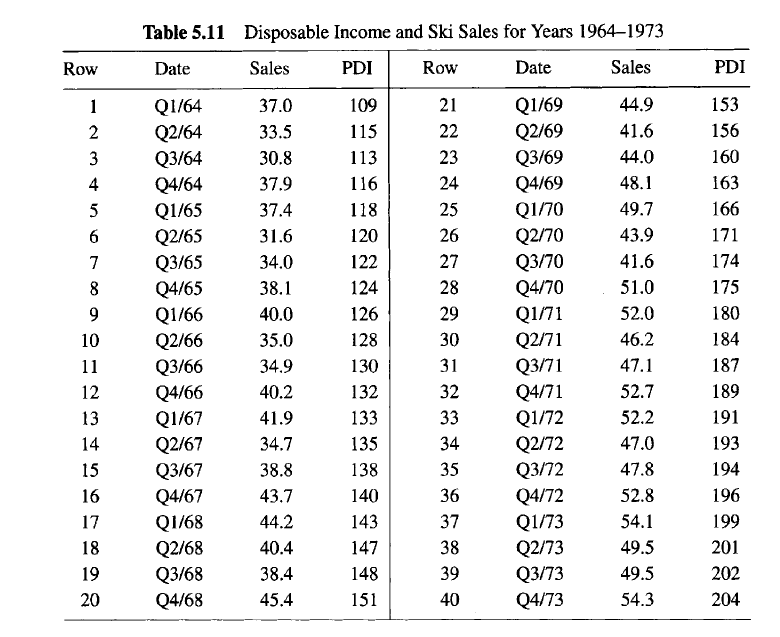
5.3 Perform a thorough analysis of the Ski Sales data in Table 5.11 using the ideas presented in Section 5.6.Table 5.11 Disposable Income and Ski Sales for Years 1964-1973 Row Date Sales PDI Row Date Sales PDI Q1/64 37.0 109 21 Q1/69 44.9 153 Q2/64 33.5 115 22 Q2/69 41.6 156 3 Q3/64 30.8 113 23 Q3/69 44.0 160 4 Q4/64 37.9 116 24 Q4/69 48.1 163 Q1/65 37.4 118 25 Q1/70 49.7 166 Q2/65 31.6 120 26 Q2/70 43.9 171 Q3/65 34.0 122 27 Q3/70 41.6 174 8 Q4/65 38.1 124 28 Q4/70 51.0 175 9 Q1/66 40.0 126 29 Q1/71 52.0 180 10 Q2/66 35.0 128 30 Q2/71 46.2 184 11 Q3/66 34.9 130 31 Q3/71 47.1 187 12 Q4/66 40.2 132 32 Q4/71 52.7 13 189 Q1/67 41.9 133 33 Q1/72 52.2 191 14 Q2/67 34.7 135 34 Q2/72 47.0 15 193 Q3/67 38.8 138 35 Q3/72 47.8 194 16 Q4/67 43.7 140 36 Q4/72 52.8 196 17 Q1/68 44.2 143 37 Q1/73 54.1 18 199 Q2/68 40.4 147 38 Q2/73 49.5 201 19 Q3/68 38.4 148 39 Q3/73 49.5 202 20 Q4/68 45.4 151 40 Q4/73 54.3 2045.6 SEASONALITY The data set we use as an example here, referred to as the Ski Sales data, is shown in Table 5.11 and can be obtained from the book's Website. The data consist of two variables: the sales, S, in millions for a firm that manufactures skis and relatedequipment for the years 1964-1973, and personal disposable income, PDI. Each of these variables is measured quarterly. We use these data in Chapter 8 to illustrate the problem of correlated errors. The model is an equation that relates S to PDI, that is, St = Po + 1PDIt + Et, where St is sales in millions in the tth period and PDI, is the corresponding personal disposable income. Our approach here is to assume the existence of a seasonal effect on sales that is determined on a quarterly basis. To measure this effect we may define indicator variables to characterize the seasonality. Since we have four quarters, we define three indicator variables, Z1, Z2, and Za, where 1, if the tth period is a first quarter, 0, otherwise, 1, if the tth period is a second quarter, 0, otherwise, 1, if the tth period is a third quarter, Z+3 = 0, otherwise. Aggregate measure of purchasing potential.The analysis and interpretation of this data set are left to the reader. The authors have analyzed these data and found that there are actually only two seasons. (See the discussion of these sales data in Chapter 8 for an analysis using only one indicator variable, two seasons.) See Kmenta (1986) for further discussion on using indicator variables for analyzing seasonality















