1. There are 24 (4!) different orders of 1, 2, 3, 4. How many orders can produce the same shape as the 2, 1, 4, 3 ?
 

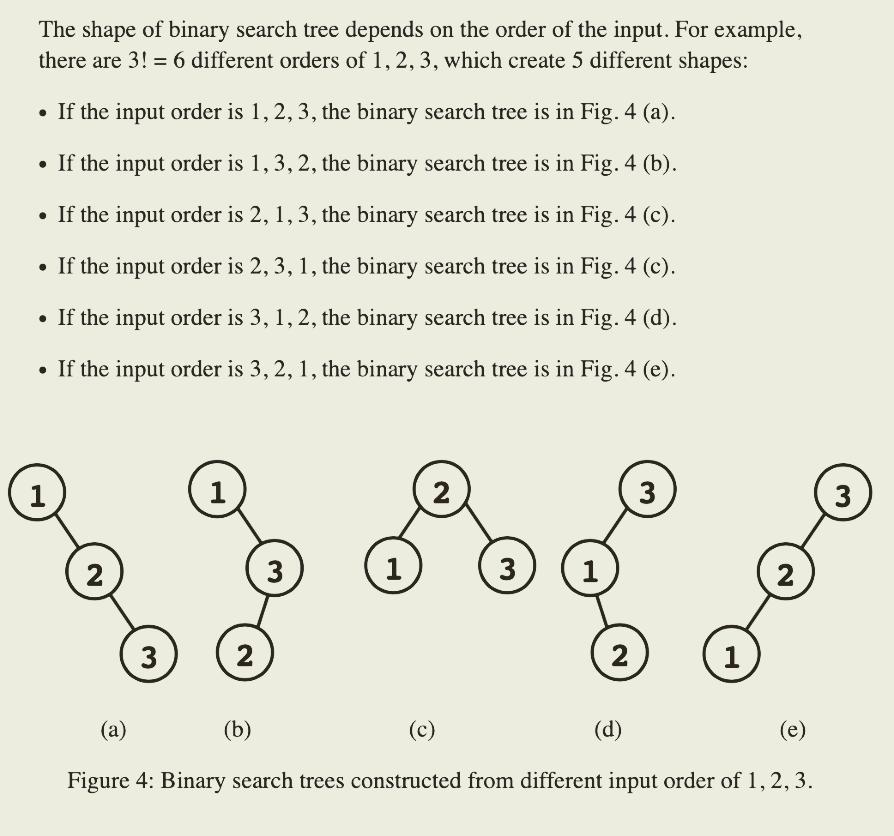
The shape of binary search tree depends on the order of the input. For example, there are 3! = 6 different orders of 1, 2, 3, which create 5 different shapes: If the input order is 1, 2, 3, the binary search tree is in Fig. 4 (a). If the input order is 1, 3, 2, the binary search tree is in Fig. 4 (b). If the input order is 2, 1, 3, the binary search tree is in Fig. 4 (c). If the input order is 2, 3, 1, the binary search tree is in Fig. 4 (c). If the input order is 3, 1, 2, the binary search tree is in Fig. 4 (d). If the input order is 3, 2, 1, the binary search tree is in Fig. 4 (e). 1 2 3 1 2 3 1 2 3 1 2 3 1 2 (a) (b) (c) (d) (e) Figure 4: Binary search trees constructed from different input order of 1, 2, 3. 3