Answered step by step
Verified Expert Solution
Question
1 Approved Answer
1. Two species compete for the same food. Develop a discrete time model that simulates their behavior. Hint, you might want to look at the
1. Two species compete for the same food. Develop a discrete time model that simulates their behavior. Hint, you might want to look at the oscillation model and the logistic model and see what each model might contribute to your answer. Provide functioning Python code to implement the model and graphical output to show the results and the phase space.
Note: the images are taken from chapter4 of the book "Introduction to the Modeling and Analysis of Complex Systems", and they are the pages (materials) mentioned in the assignment.

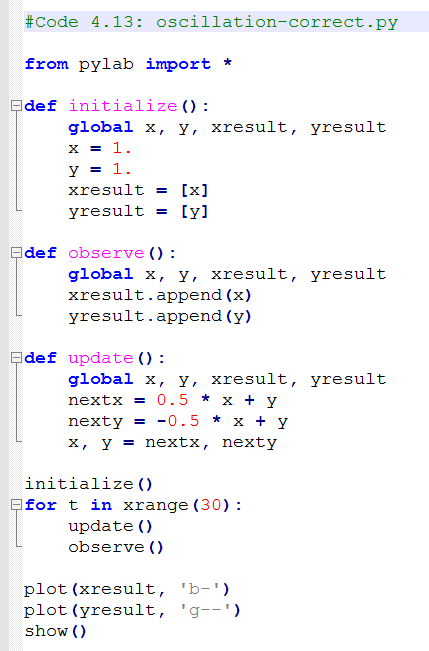
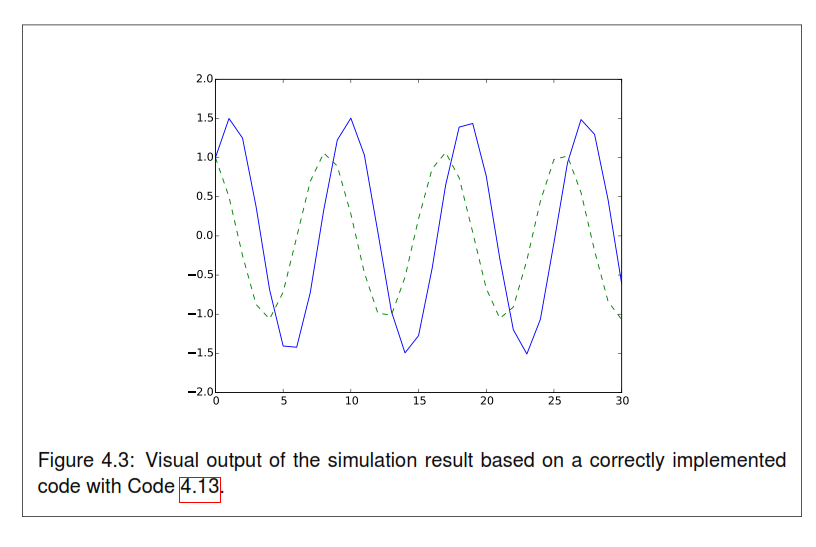
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


