Question: Two random variables X and Y have a joint cumulative distribution function given by FXY(x, y) = 1/2 [u(x-2) + u(x-3)] {(1 - exp(-y/2))
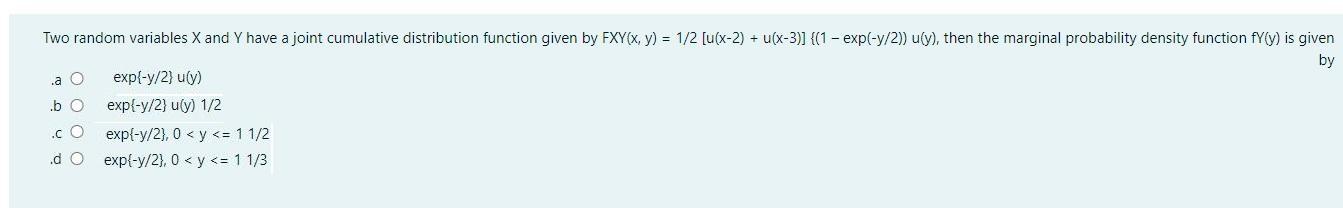
![given by FXY(x, y) = 1/2 [u(x-2) + u(x-3)] {(1 - exp(-y/2))](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2021/02/6035f4148d613_1614148625639.jpg)
Two random variables X and Y have a joint cumulative distribution function given by FXY(x, y) = 1/2 [u(x-2) + u(x-3)] {(1 - exp(-y/2)) u(y), then the marginal probability density function fY(y) is given by .a C exp{-y/2} u(y) .b O exp{-y/2} u(y) 1/2 exp{-y/2}, 0 < y A random process X(t) = A cos(wt) + B sin(wt), where A and B are two random variables, then X(t) is stationary if All the mentioned .a O E[AB] = 0.b O E[A? ] = E[B? ].c O = E[B] = 0.d O E[A]
Step by Step Solution
3.42 Rating (149 Votes )
There are 3 Steps involved in it
1 As per the given function and by utilizing the J... View full answer

Get step-by-step solutions from verified subject matter experts


