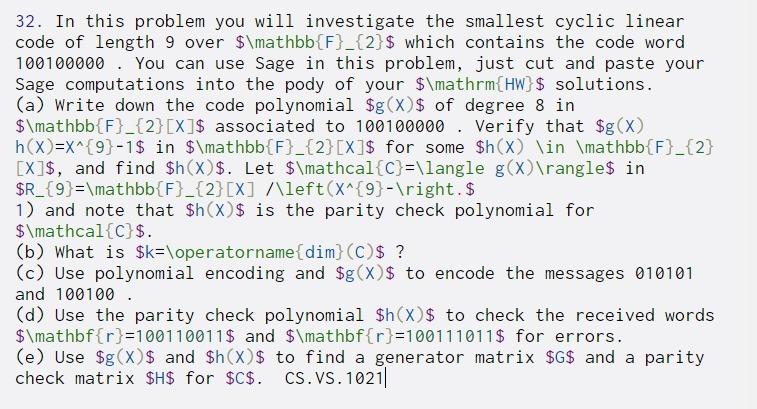
32. In this problem you will investigate the smallest cyclic linear code of length 9 over $\mathbb{F}_{2}$ which contains the code word 100100000 . You can use Sage in this problem, just cut and paste your Sage computations into the pody of your $\mathrm{HW} $ solutions. (a) Write down the code polynomial $g(x)$ of degree 8 in $\mathbb{F}_{2}[X]$ associated to 100100000 . Verify that $g(X) h(X)=X^{9}-1$ in $\mathbb{F}_{2}[X]$ for some $h(x) \in \mathbb{F}_{2} [X]$, and find $h(x) $. Let $\mathcal{C}=\langle g(x) angle$ in $R_{9}=\mathbb{F}_{2}[X] /\left(X^{9}- ight. $ 1) and note that $h(X$ is the parity check polynomial for $\mathcal{C}$. (b) What is $k=\operatorname{dim}(C)$ ? (c) Use polynomial encoding and $g(x)$ to encode the messages 010101 and 100100. (d) Use the parity check polynomial $h(x) $ to check the received words $\mathbf{r}=100110011$ and $\mathbf{r}=100111011$ for errors. (e) Use $g(x)$ and $h(x) $ to find a generator matrix $G$ and a parity check matrix $H$ for $C$. CS.VS.1021|