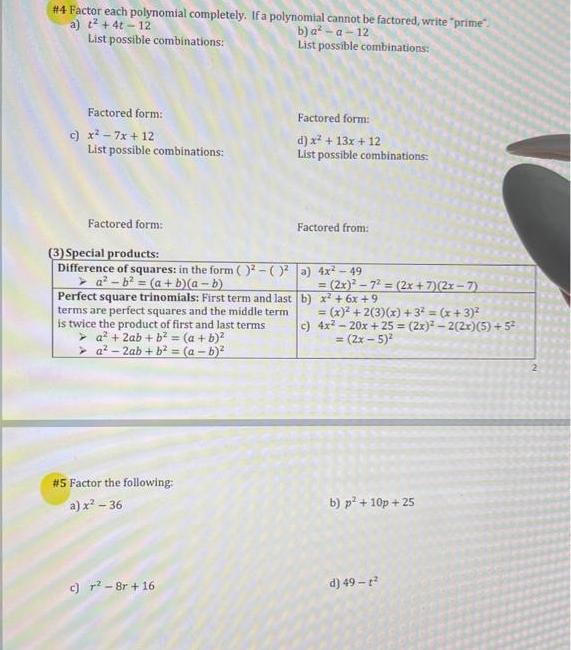
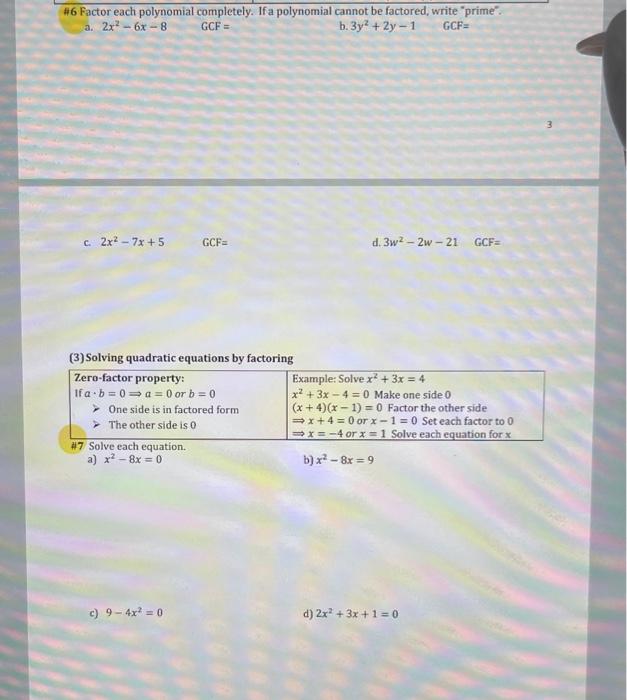
#4 Factor each polynomial completely. If a polynomial cannot be factored, write "prime". a) t + 4t-12 b) a-a-12 List possible combinations: List possible combinations: Factored form: c) x - 7x+12 List possible combinations: Factored form: (3) Special products: Difference of squares: in the form ()-() ab = (a + b)(a - b) Perfect square trinomials: First term and last terms are perfect squares and the middle term is twice the product of first and last terms > a + 2ab + b = (a + b) a-2ab + b = (a - b) #5 Factor the following: a) x - 36 c) r-8r+16 Factored form: d) x + 13x + 12 List possible combinations: Factored from: a) 4x - 49 = (2x)-7 = (2x + 7)(2x-7) x + 6x +9 b) c) = (x) + 2(3)(x) +3 = (x+3) 4x - 20x + 25 = (2x)-2(2x)(5) +5 = (2x - 5) b) p + 10p +25 d) 49- 2 #6 Factor each polynomial completely. If a polynomial cannot be factored, write "prime". a. 2x - 6x-8 GCF = b. 3y + 2y-1 GCF= c. 2x - 7x+5 (3) Solving quadratic equations by factoring Zero-factor property: Ifa.b=0a=0 or b=0 GCF= One side is in factored form The other side is 0 #7 Solve each equation. a) x - 8x = 0 c) 9-4x = 0 d. 3w-2w-21 GCF= Example: Solve x + 3x = 4 x + 3x -4 = 0 Make one side 0 (x+4)(x-1)= 0 Factor the other side x+4= 0 orx-1=0 Set each factor to 0 x=-4 or x = 1 Solve each equation for x b) x - 8x = 9 d) 2x + 3x + 1 = 0