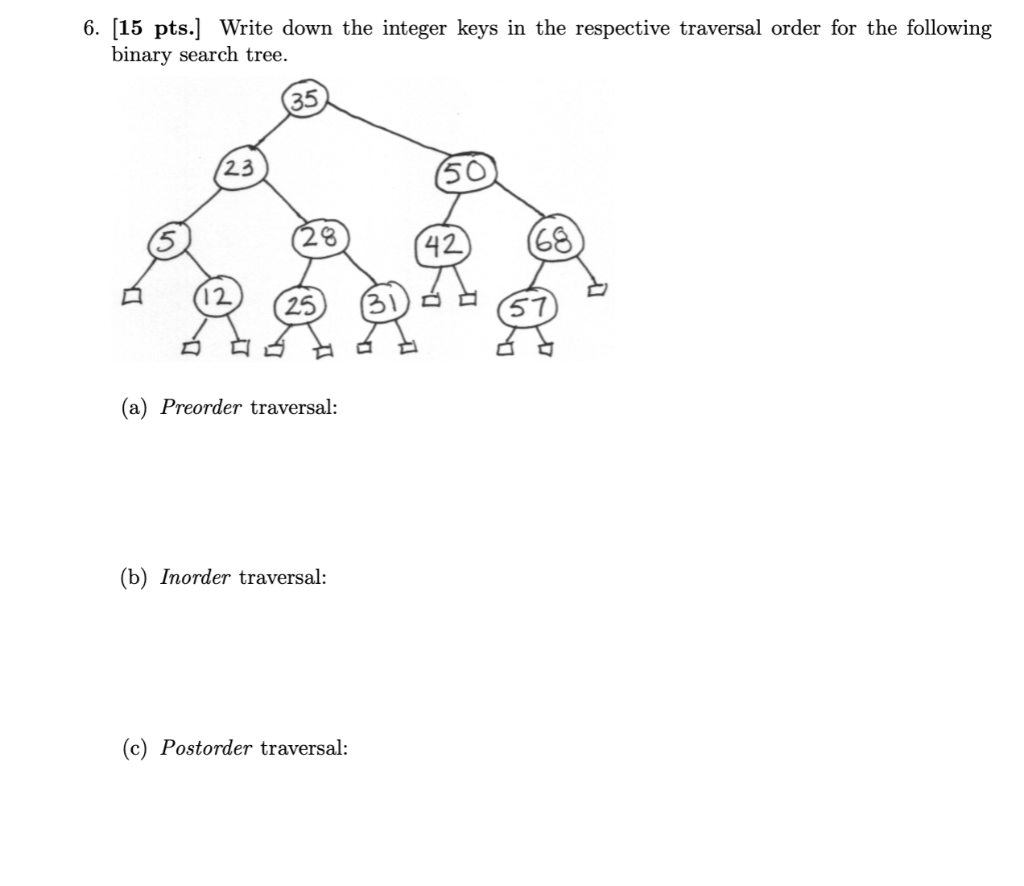
5. (14 pts.] Consider the typical matrix-vector multiplication operation: given a (d * d) matrix A (i.e., a squared matrix with d rows and d columns), and a d-dimensional (row) vector x (i.e., a vector with d elements; or equivalently, a matrix with d rows and a single column), where d is a positive integer, compute the d-dimensional (row) vector y = Ar. That is, using O-based indexing, for all i = 0,1, ..., d-1, yi = L == dij;, where dij is the element in the ith row and jth column of matrix A. Consider the following algorithm, MATRIXVECMULT (Algorithm 5), for this operation, assumming that A and x are represented using 2-dimensional and 1- dimensional arrays, respectively, as typically done. The algorithm uses an auxiliary algorithm, VECMULT (Algorithm 6), which takes as input two arrays of numbers, z and x, and a positive integer d, where the size of both z and x is at least d. Assume that the input to this auxiliary algorithm VECMULT (Algorithm 6) is passed by-value. Algorithm 5 MATRIX VECMULT(A, x,d) 1: yt new 1-dim array of d numbers 2: zt new 1-dim array of d numbers 3: for it to d - 1 do for jo to d-1 do 5: z[j] + A[i][j] 6: y[i] + VECMULT(z, x,d) 7: return y 4: Algorithm 6 VECMULT(2, 3, d) 1: if d=0 then return 0 2: return z[d 1] * x[d 1] + VECMULT(z, x, d 1) (a) Provide the tightest characterization possible of the running time and space complexity of the algorithm MATRIXVECMULT (Algorithm 5), using either big-Oh and big-Omega, or simply big-Theta, as a function of the input value d. Time Space (b) Provide the tightest characterization possible of the running time and space complexity of the same algorithm MATRIXVECMULT (Algorithm 5), using either big-Oh and big- Omega, or simply big-Theta, now as a function of the input size n; that is, n characterizes the size of the input to the algorithm as a function of the input value d. Time Space (c) Is this a linear-time algorithm? Please circle your answer and explain briefly but clearly. In addition, if you answered 'No', please clearly state what type of algorithm it is in terms of running time. Yes No (d) Please write, using pseudocode, a linear-time and linear-space algorithm for the same task. 6. (15 pts.] Write down the integer keys in the respective traversal order for the following binary search tree. 35 23 (50 (42) 68 25 (a) Preorder traversal: (b) Inorder traversal: (c) Postorder traversal: 5. (14 pts.] Consider the typical matrix-vector multiplication operation: given a (d * d) matrix A (i.e., a squared matrix with d rows and d columns), and a d-dimensional (row) vector x (i.e., a vector with d elements; or equivalently, a matrix with d rows and a single column), where d is a positive integer, compute the d-dimensional (row) vector y = Ar. That is, using O-based indexing, for all i = 0,1, ..., d-1, yi = L == dij;, where dij is the element in the ith row and jth column of matrix A. Consider the following algorithm, MATRIXVECMULT (Algorithm 5), for this operation, assumming that A and x are represented using 2-dimensional and 1- dimensional arrays, respectively, as typically done. The algorithm uses an auxiliary algorithm, VECMULT (Algorithm 6), which takes as input two arrays of numbers, z and x, and a positive integer d, where the size of both z and x is at least d. Assume that the input to this auxiliary algorithm VECMULT (Algorithm 6) is passed by-value. Algorithm 5 MATRIX VECMULT(A, x,d) 1: yt new 1-dim array of d numbers 2: zt new 1-dim array of d numbers 3: for it to d - 1 do for jo to d-1 do 5: z[j] + A[i][j] 6: y[i] + VECMULT(z, x,d) 7: return y 4: Algorithm 6 VECMULT(2, 3, d) 1: if d=0 then return 0 2: return z[d 1] * x[d 1] + VECMULT(z, x, d 1) (a) Provide the tightest characterization possible of the running time and space complexity of the algorithm MATRIXVECMULT (Algorithm 5), using either big-Oh and big-Omega, or simply big-Theta, as a function of the input value d. Time Space (b) Provide the tightest characterization possible of the running time and space complexity of the same algorithm MATRIXVECMULT (Algorithm 5), using either big-Oh and big- Omega, or simply big-Theta, now as a function of the input size n; that is, n characterizes the size of the input to the algorithm as a function of the input value d. Time Space (c) Is this a linear-time algorithm? Please circle your answer and explain briefly but clearly. In addition, if you answered 'No', please clearly state what type of algorithm it is in terms of running time. Yes No (d) Please write, using pseudocode, a linear-time and linear-space algorithm for the same task. 6. (15 pts.] Write down the integer keys in the respective traversal order for the following binary search tree. 35 23 (50 (42) 68 25 (a) Preorder traversal: (b) Inorder traversal: (c) Postorder traversal