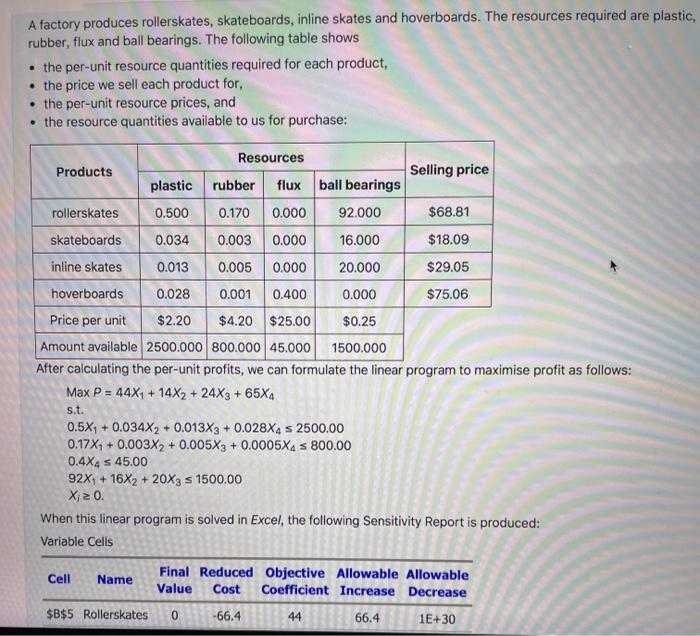
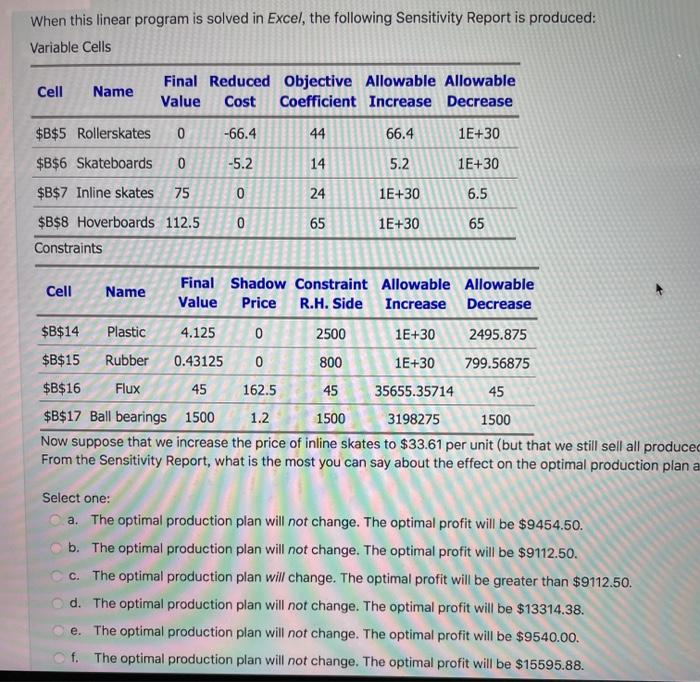
A factory produces rollerskates, skateboards, inline skates and hoverboards. The resources required are plastic, rubber, flux and ball bearings. The following table shows . the per-unit resource quantities required for each product, the price we sell each product for, the per-unit resource prices, and the resource quantities available to us for purchase: Resources Products Selling price plastic rubber flux ball bearings rollerskates 0.500 0.170 0.000 92.000 $68.81 skateboards 0.034 0.003 0.000 16.000 $18.09 inline skates 0.013 0.005 0.000 20.000 $29.05 hoverboards 0.028 0.001 0.400 0.000 $75.06 Price per unit $2.20 $4.20 $25.00 $0.25 Amount available 2500.000 800.000 45.000 1500.000 After calculating the per-unit profits, we can formulate the linear program to maximise profit as follows: Max P = 44X1 + 14X2 + 24X3 + 65X4 s.t. 0.5X1 + 0.034X2 + 0.013X3 + 0.028X4 s 2500.00 0.17X, + 0.003X2 + 0.005X3 + 0.0005X4 S 800.00 0.4X4 5 45.00 92X1 + 16X2 + 20X3 s 1500.00 Xi20. When this linear program is solved in Excel, the following Sensitivity Report is produced: Variable Cells Cell Name Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 0 -66.4 44 66.4 1E+30 $B$5 Rollerskates When this linear program is solved in Excel, the following Sensitivity Report is produced: Variable Cells Cell Name Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease $B$5 Rollerskates 0 -66.4 44 66.4 1E+30 $B$6 Skateboards 0 -5.2 14 5.2 1E+30 $B$7 Inline skates 75 0 24 1E+30 6.5 0 65 1E+30 65 $B$8 Hoverboards 112.5 Constraints Cell Name Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease $B$14 Plastic 4.125 0 2500 1E+30 2495.875 $B$15 Rubber 0.43125 0 800 1E+30 799.56875 $B$16 Flux 45 162.5 45 35655.35714 45 $B$17 Ball bearings 1500 1.2 1500 3198275 1500 Now suppose that we increase the price of inline skates to $33.61 per unit (but that we still sell all produced From the Sensitivity Report, what is the most you can say about the effect on the optimal production plan a Select one: a. The optimal production plan will not change. The optimal profit will be $9454.50. b. The optimal production plan will not change. The optimal profit will be $9112.50. C. The optimal production plan will change. The optimal profit will be greater than $9112.50. d. The optimal production plan will not change. The optimal profit will be $13314.38. e. The optimal production plan will not change. The optimal profit will be $9540.00. f. The optimal production plan will not change. The optimal profit will be $15595.88