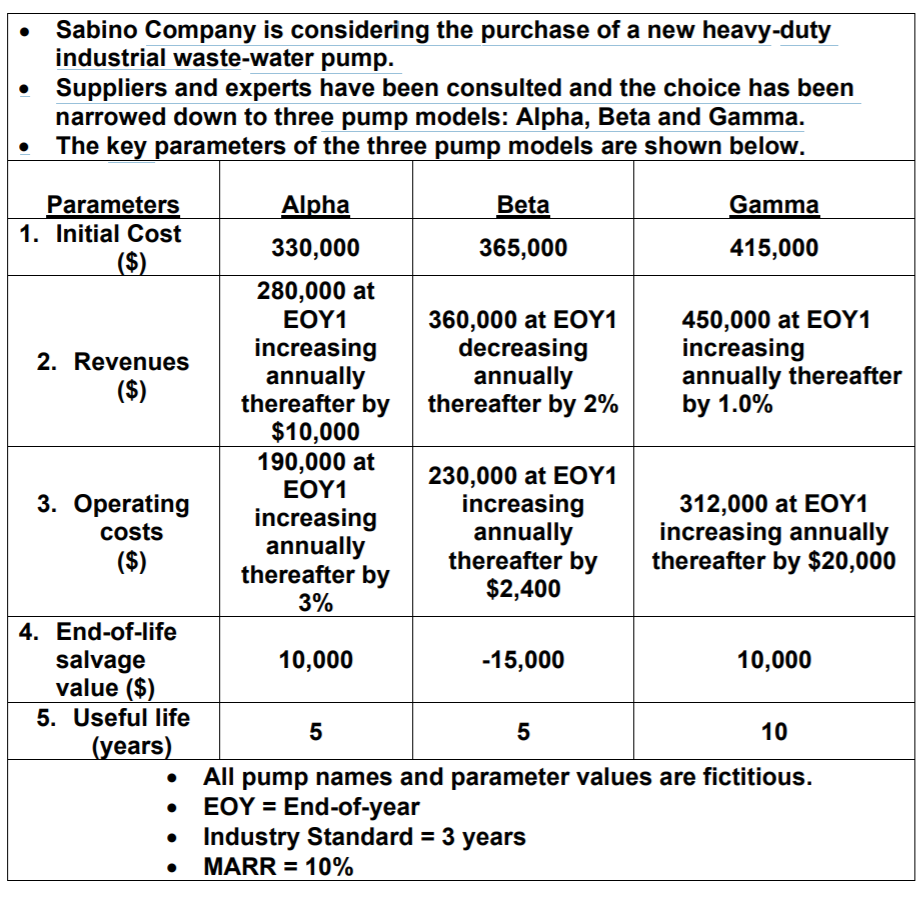
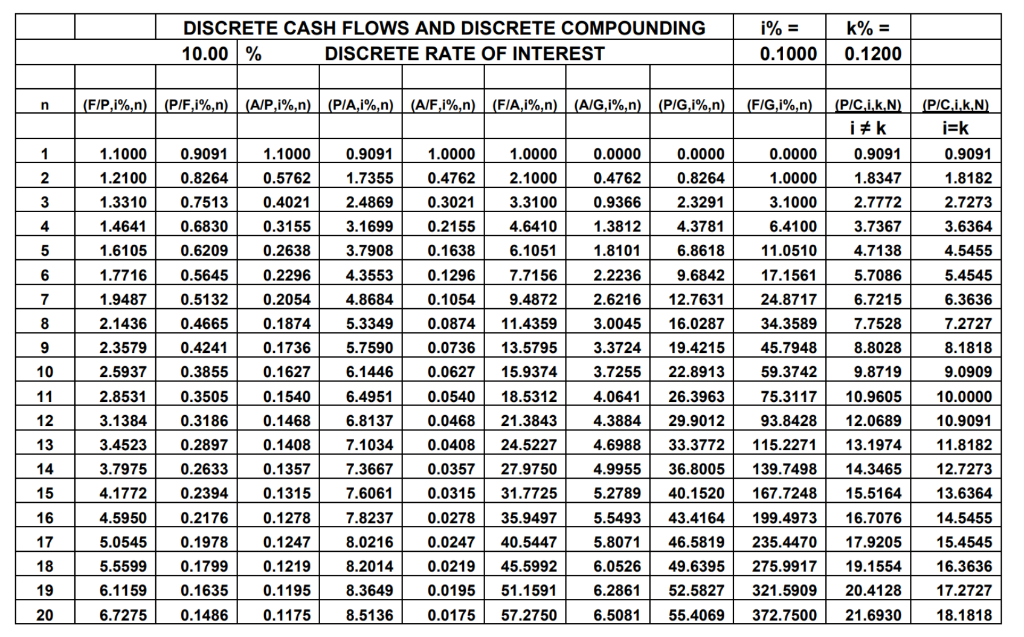
Answer the following questions below using the 1st table that describes the Project/Investement Details. Ensure to include your steps. Use the "Discrete cash flow and discrete compounding" table and use notation such as (A/G, 10%, n) (A/P, 10%, n) (F/P, 10%, n) in your steps.

29. If Sabino Company purchased two pumps in the calendar year 2021 (one pump in January and the other in September), which pump should it purchase in January?

30. Erica plans to make the following bank deposits in 2021: $600 on March 31 $800 on June 30 $1,000 on September 30 $1,200 on December 31. Which answer option below would give Ericas bank balance on December 31, 2021 if the banks interest rate were 12% compounded semi-annually? (Note that Ericas December 31 deposit would be included in her yearend bank balance). a) [600+200(A/G,6%,4)](A/P,6%,4)(F/A,6%,4) b) {600(F/P,6%,9)+800(F/P,6%,6)+1,000(F/P,6%,3)+1,200 c) {600+800+1,000}(F/P,6%,1)+1,200 d) None of these answers is correct.

31. Bonus Question (2 points): Incremental ERR Calculation

If detailed steps are shown and the answers are correct, I will award a like!

Sabino Company is considering the purchase of a new heavy-duty industrial waste-water pump. Suppliers and experts have been consulted and the choice has been narrowed down to three pump models: Alpha, Beta and Gamma. The key parameters of the three pump models are shown below. Parameters Alpha Beta Gamma 1. Initial Cost 330,000 365,000 415,000 ($) 280,000 at EOY1 360,000 at EOY1 450,000 at EOY1 increasing decreasing increasing 2. Revenues annually annually ($) annually thereafter thereafter by thereafter by 2% by 1.0% $10,000 190,000 at 230,000 at EOY1 EOY1 3. Operating increasing increasing 312,000 at EOY1 costs annually increasing annually ($) annually thereafter by thereafter by $20,000 thereafter by $2,400 3% 4. End-of-life salvage 10,000 -15,000 10,000 value ($) 5. Useful life 5 5 10 (years) All pump names and parameter values are fictitious. EOY = End-of-year Industry Standard = 3 years MARR = 10% DISCRETE CASH FLOWS AND DISCRETE COMPOUNDING 10.00% DISCRETE RATE OF INTEREST i% = 0.1000 k% = 0.1200 n (F/P,i%,n) (P/F,i%n) (A/P,i%,n) (PIA,i%,n) (A/F,i%,n) (FIA,i%,n) (A/Gi%n) (P/Gi%,n) (F/G,i%,n) 1 0.9091 0.9091 1.0000 0.0000 0.0000 1.0000 0.4762 0.0000 0.4762 2 0.8264 1.1000 1.2100 1.3310 1.4641 1.6105 1.1000 0.5762 0.4021 0.3155 (PIC.i.k.n) i #k 0.9091 1.8347 2.7772 3.7367 4.7138 1.7355 2.4869 3.1699 3.7908 3 (P/C.I.K.N) i=k 0.9091 1.8182 2.7273 3.6364 4.5455 0.3021 0.2155 4 2.3291 4.3781 6.8618 5 0.2638 0.1638 6 4.3553 0.1296 5.4545 7 4.8684 0.1054 8 0.8264 0.7513 0.6830 0.6209 0.5645 0.5132 0.4665 0.4241 0.3855 0.3505 0.3186 0.2897 0.2633 0.2394 0.0874 0.0736 6.3636 7.2727 8.1818 9 10 5.3349 5.7590 6.1446 6.4951 6.8137 0.0627 1.0000 3.1000 6.4100 11.0510 17.1561 24.8717 34.3589 45.7948 59.3742 75.3117 93.8428 115.2271 139.7498 167.7248 1.7716 1.9487 2.1436 2.3579 2.5937 2.8531 3.1384 3.4523 3.7975 4.1772 4.5950 5.0545 5.5599 6.1159 6.7275 0.2296 0.2054 0.1874 0.1736 0.1627 0.1540 0.1468 0.1408 0.1357 0.1315 0.1278 0.1247 11 0.9366 1.3812 1.8101 2.2236 2.6216 3.0045 3.3724 3.7255 4.0641 4.3884 4.6988 4.9955 5.2789 5.5493 5.8071 6.0526 2.1000 3.3100 4.6410 6.1051 7.7156 9.4872 11.4359 13.5795 15.9374 18.5312 21.3843 24.5227 27.9750 31.7725 35.9497 40.5447 45.5992 51.1591 57.2750 9.6842 12.7631 16.0287 19.4215 22.8913 26.3963 29.9012 33.3772 36.8005 40.1520 43.4164 AWN 0.0540 0.0468 0.0408 0.0357 0.0315 0.0278 0.0247 0.0219 0.0195 0.0175 15 5.7086 6.7215 7.7528 8.8028 9.8719 10.9605 12.0689 13.1974 14.3465 15.5164 16.7076 17.9205 19.1554 20.4128 21.6930 7.1034 7.3667 7.6061 7.8237 8.0216 8.2014 8.3649 9.0909 10.0000 10.9091 11.8182 12.7273 13.6364 14.5455 15.4545 16.3636 17.2727 18.1818 16 0.2176 17 18 0.1219 0.1978 0.1799 0.1635 0.1486 46.5819 49.6395 52.5827 55.4069 199.4973 235.4470 275.9917 321.5909 372.7500 19 0.1195 6.2861 6.5081 20 0.1175 8.5136 . . You will find several (more than one) negative cash flows when calculating the differences between the net cash inflows of two projects. As a result, the calculation of the incremental ERR is no longer direct as the calculated external rate of return (i*) must be used for all negative cash flow differences. Using Excel's Solver add-in function, determine the incremental external rate of return between the Alpha and Gamma investments. In the example below, MARR (usually 10% for our purposes) cannot be used to calculate the future value of the negative cash flow differences at EOYO, EOY3 and EOY4. Use the ERR (i*) to bring all negative cash flow differences to EOY5 and MARR (=10%) to bring all positive cash flow differences to EOY5. Find the ERR (i.e., i*) which sets the future worth of negative cash flow differences equal to that of the positive cash flow differences between the Alpha and Gamma pumps. With more than one negative cash flow difference, the answer obtained with Excel's MIRR function will be different (and incorrect) from the answer obtained with Excel's Solver. Sabino Company is considering the purchase of a new heavy-duty industrial waste-water pump. Suppliers and experts have been consulted and the choice has been narrowed down to three pump models: Alpha, Beta and Gamma. The key parameters of the three pump models are shown below. Parameters Alpha Beta Gamma 1. Initial Cost 330,000 365,000 415,000 ($) 280,000 at EOY1 360,000 at EOY1 450,000 at EOY1 increasing decreasing increasing 2. Revenues annually annually ($) annually thereafter thereafter by thereafter by 2% by 1.0% $10,000 190,000 at 230,000 at EOY1 EOY1 3. Operating increasing increasing 312,000 at EOY1 costs annually increasing annually ($) annually thereafter by thereafter by $20,000 thereafter by $2,400 3% 4. End-of-life salvage 10,000 -15,000 10,000 value ($) 5. Useful life 5 5 10 (years) All pump names and parameter values are fictitious. EOY = End-of-year Industry Standard = 3 years MARR = 10% DISCRETE CASH FLOWS AND DISCRETE COMPOUNDING 10.00% DISCRETE RATE OF INTEREST i% = 0.1000 k% = 0.1200 n (F/P,i%,n) (P/F,i%n) (A/P,i%,n) (PIA,i%,n) (A/F,i%,n) (FIA,i%,n) (A/Gi%n) (P/Gi%,n) (F/G,i%,n) 1 0.9091 0.9091 1.0000 0.0000 0.0000 1.0000 0.4762 0.0000 0.4762 2 0.8264 1.1000 1.2100 1.3310 1.4641 1.6105 1.1000 0.5762 0.4021 0.3155 (PIC.i.k.n) i #k 0.9091 1.8347 2.7772 3.7367 4.7138 1.7355 2.4869 3.1699 3.7908 3 (P/C.I.K.N) i=k 0.9091 1.8182 2.7273 3.6364 4.5455 0.3021 0.2155 4 2.3291 4.3781 6.8618 5 0.2638 0.1638 6 4.3553 0.1296 5.4545 7 4.8684 0.1054 8 0.8264 0.7513 0.6830 0.6209 0.5645 0.5132 0.4665 0.4241 0.3855 0.3505 0.3186 0.2897 0.2633 0.2394 0.0874 0.0736 6.3636 7.2727 8.1818 9 10 5.3349 5.7590 6.1446 6.4951 6.8137 0.0627 1.0000 3.1000 6.4100 11.0510 17.1561 24.8717 34.3589 45.7948 59.3742 75.3117 93.8428 115.2271 139.7498 167.7248 1.7716 1.9487 2.1436 2.3579 2.5937 2.8531 3.1384 3.4523 3.7975 4.1772 4.5950 5.0545 5.5599 6.1159 6.7275 0.2296 0.2054 0.1874 0.1736 0.1627 0.1540 0.1468 0.1408 0.1357 0.1315 0.1278 0.1247 11 0.9366 1.3812 1.8101 2.2236 2.6216 3.0045 3.3724 3.7255 4.0641 4.3884 4.6988 4.9955 5.2789 5.5493 5.8071 6.0526 2.1000 3.3100 4.6410 6.1051 7.7156 9.4872 11.4359 13.5795 15.9374 18.5312 21.3843 24.5227 27.9750 31.7725 35.9497 40.5447 45.5992 51.1591 57.2750 9.6842 12.7631 16.0287 19.4215 22.8913 26.3963 29.9012 33.3772 36.8005 40.1520 43.4164 AWN 0.0540 0.0468 0.0408 0.0357 0.0315 0.0278 0.0247 0.0219 0.0195 0.0175 15 5.7086 6.7215 7.7528 8.8028 9.8719 10.9605 12.0689 13.1974 14.3465 15.5164 16.7076 17.9205 19.1554 20.4128 21.6930 7.1034 7.3667 7.6061 7.8237 8.0216 8.2014 8.3649 9.0909 10.0000 10.9091 11.8182 12.7273 13.6364 14.5455 15.4545 16.3636 17.2727 18.1818 16 0.2176 17 18 0.1219 0.1978 0.1799 0.1635 0.1486 46.5819 49.6395 52.5827 55.4069 199.4973 235.4470 275.9917 321.5909 372.7500 19 0.1195 6.2861 6.5081 20 0.1175 8.5136 . . You will find several (more than one) negative cash flows when calculating the differences between the net cash inflows of two projects. As a result, the calculation of the incremental ERR is no longer direct as the calculated external rate of return (i*) must be used for all negative cash flow differences. Using Excel's Solver add-in function, determine the incremental external rate of return between the Alpha and Gamma investments. In the example below, MARR (usually 10% for our purposes) cannot be used to calculate the future value of the negative cash flow differences at EOYO, EOY3 and EOY4. Use the ERR (i*) to bring all negative cash flow differences to EOY5 and MARR (=10%) to bring all positive cash flow differences to EOY5. Find the ERR (i.e., i*) which sets the future worth of negative cash flow differences equal to that of the positive cash flow differences between the Alpha and Gamma pumps. With more than one negative cash flow difference, the answer obtained with Excel's MIRR function will be different (and incorrect) from the answer obtained with Excel's Solver