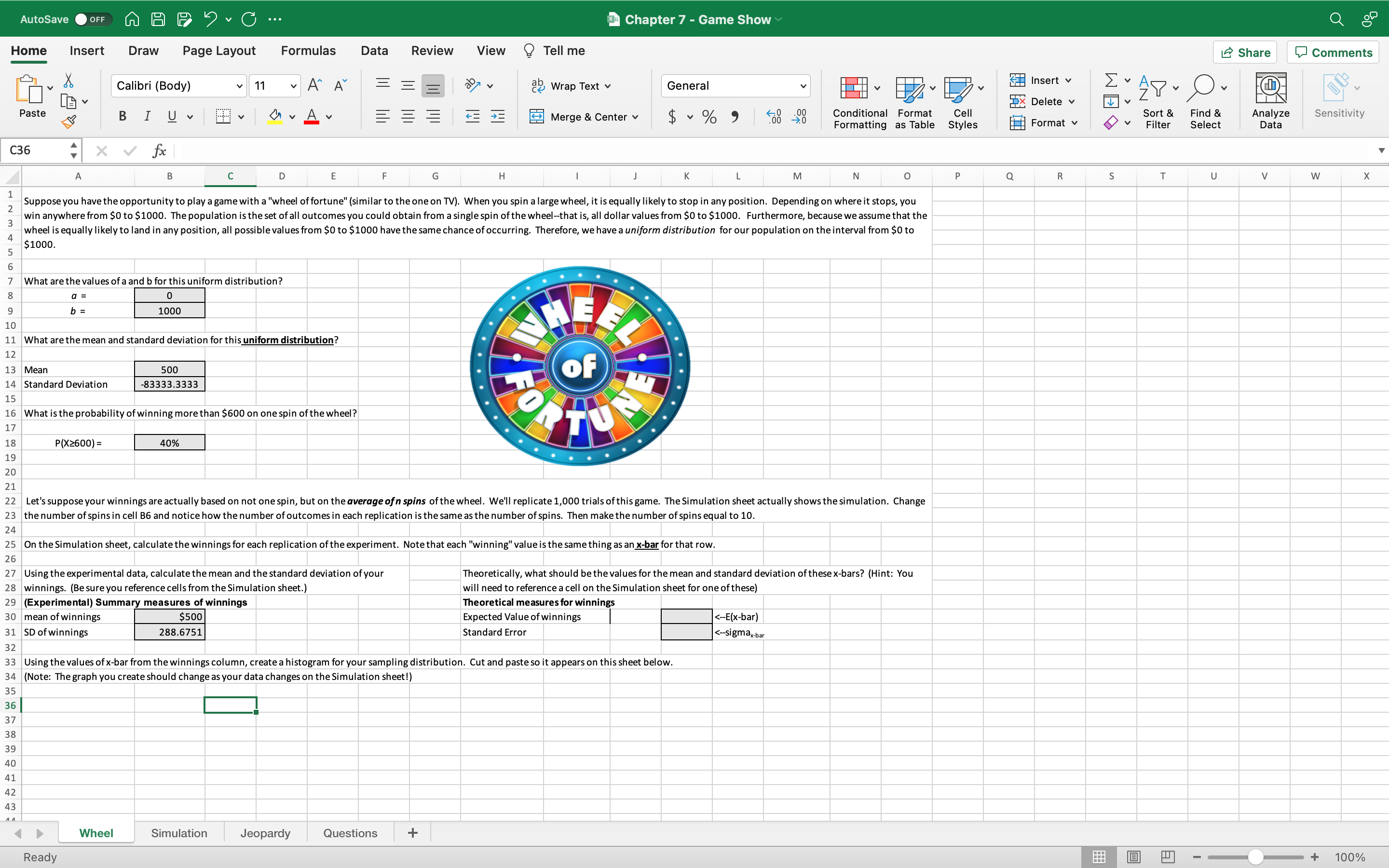
AutoSave OFF WA FIC ... Chapter 7 - Game Show Home Insert Draw Page Layout Formulas Data Review View ? Tell me I Share Comments Calibri (Body) v 11 AA ab Wrap Text General Insert v Ex AP- O. Ex Delete v I V Z Paste BIUV DV Av E E Merge & Center v $ ~ % " Conditional Format Cell Sort & Find & Analyze Sensitivity Formatting as Table Styles Format v Filter Select Data C36 X V fx A B C D E G H K M N 0 Q R S T U W X Suppose you have the opportunity to play a game with a "wheel of fortune" (similar to the one on TV). When you spin a large wheel, it is equally likely to stop in any position. Depending on where it stops, you W N win anywhere from $0 to $1000. The population is the set of all outcomes you could obtain from a single spin of the wheel--that is, all dollar values from $0 to $1000. Furthermore, because we assume that the wheel is equally likely to land in any position, all possible values from $0 to $1000 have the same chance of occurring. Therefore, we have a uniform distribution for our population on the interval from $0 to $1000. 7 What are the values of a and b for this uniform distribution? . b= 1000 E 10 11 What are the mean and standard deviation for this uniform distribution? 12 13 Mean 500 OF 14 Standard Deviation -83333.3333 15 16 What is the probability of winning more than $600 on one spin of the wheel? 17 18 P(X2600) = 40% 19 . 20 21 22 Let's suppose your winnings are actually based on not one spin, but on the average of n spins of the wheel. We'll replicate 1,000 trials of this game. The Simulation sheet actually shows the simulation. Change the number of spins in cell B6 and notice how the number of outcomes in each replication is the same as the number of spins. Then make the number of spins equal to 10. 24 25 On the Simulation sheet, calculate the winnings for each replication of the experiment. Note that each "winning" value is the same thing as an x-bar for that row. 26 Using the experimental data, calculate the mean and the standard deviation of your Theoretically, what should be the values for the mean and standard deviation of these x-bars? (Hint: You 28 winnings. (Be sure you reference cells from the Simulation sheet.) will need to reference a cell on the Simulation sheet for one of these 29 (Experimental) Summary measures of winnings Theoretical measures for winnings 30 mean of winnings $500 Expected Value of winnings