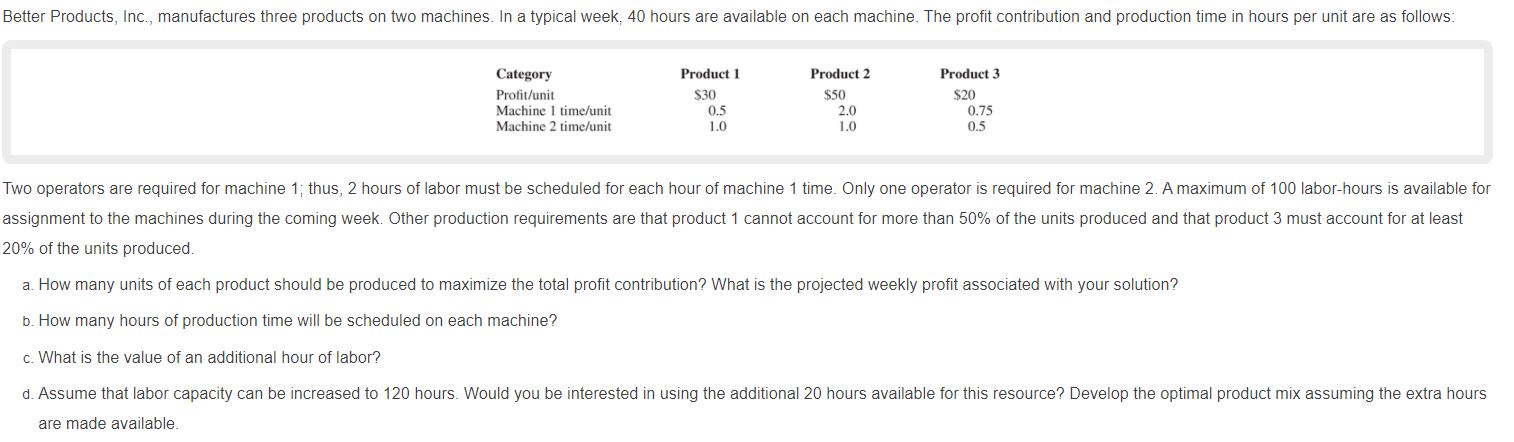
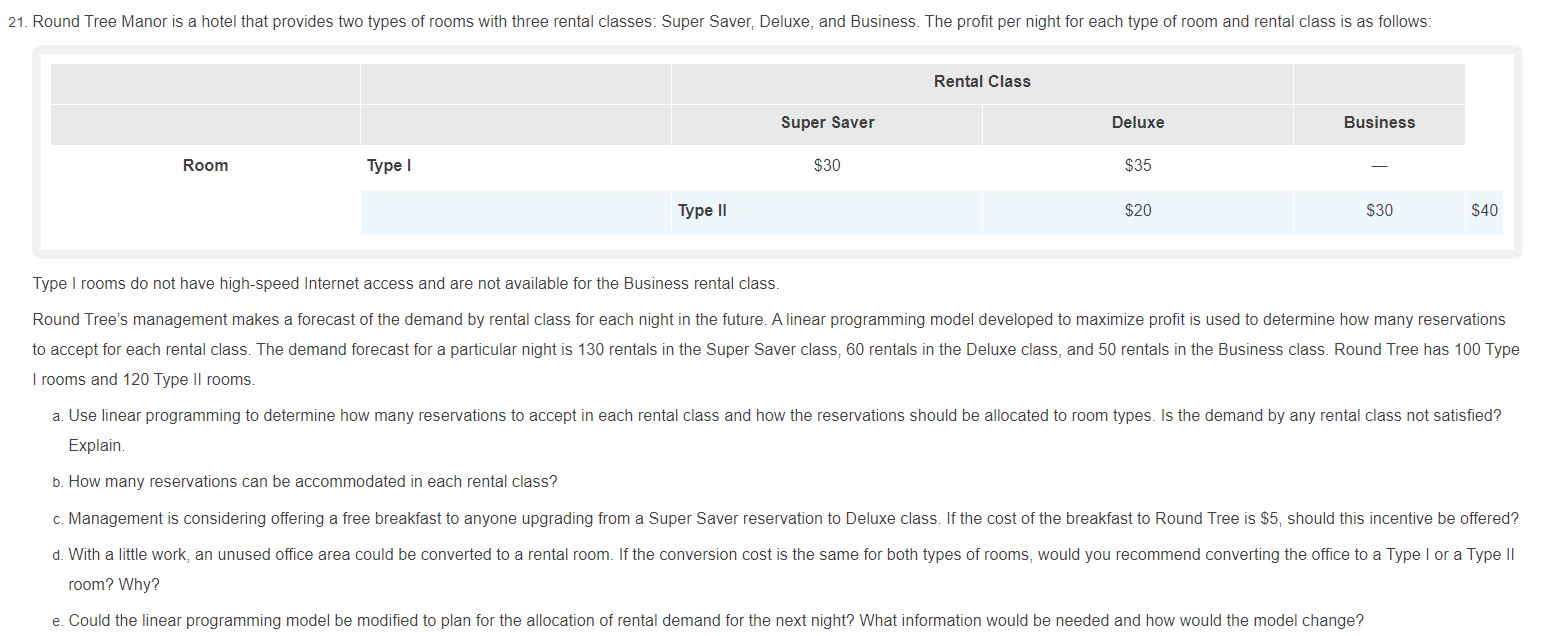
Better Products, Inc, manutactures three products on two machines. In a typical week, 40 hours are available on each machine. The prot contribution and production time in hours per unit are as follows: Category Product I Product 2 Product 3 Proh'unit 530 $50 $20 Machine I limu'nnit 05 2.0 0.75 Machine 2 u'mcinnil LO LO 0.5 Two operators are required for machine 1. thus, 2 hours otlabor must be scheduled for each hour of machine 1 time. Only one operator is required for machine 2 Amaximum of 100 laborhours is available for assignment to the machines during the coming week Other production requirements are that product 1 cannot account for more than 50% of the units produced and that product 3 must account for at least 20% of the units produced. a. How many units of each product should be produced to maximize the total prot contribution? What Is the projected weekly prot associated with your solution? b. How many hours of production time will be scheduled on each machine? c. What is the value of an additional hour of labor? a. Assume that labor capacity can be increased to 120 hours. Would you be interested in using the additional 20 hours available for this resource? Develop the optimal product mix assuming the extra hours are made available. 21, Round Tree Manor is a hotel that provides two types of rooms with three rental classes Super Saver, Deluxe, and Business The prot per night for each type of room and rental class is as follows: Rental Class Super Saver Deluxe Business Room Type | 5530 $35 7 Type II $20 $30 $130 Type | rooms do not have high-speed internet access and are not available for the Business rental class. Round Tree's management makes a forecast of the demand by rental class for each night in the future, A linear programming model developed to maXImize profit is used to determine how many reservations to accept for each rental class. The demand forecast for a particular night is 130 rentals in the Super Saver class, 60 rentals in the Deluxe class, and 50 rentais in the Business class. Round Tree has 100 Type | rooms and 120 Type II rooms a. Use linear programming to determine how many reservations to accept in each rentat class and how the reservations shoutd be allocated to room types. Is the demand by any rental class not satised? Explain D How many reservations can be accommodated in each rental class? c. Management is conSidering offering a free breakfast to anyone upgrading from a Super Saver reservation to Deluxe class lf the cost of the breakfast to Round Tree is $5, should this incentive be offered? a. With a little work' an unused otTice area could be converted to a rental room. lfthe conversion cost is the same for both types of rooms, would you recommend converting the ofce to a Type | or a Type II room? Why? e Could the linear programming model be modied to ptan for the allocation ot rental demand for the next night? What information would be needed and how would the model change