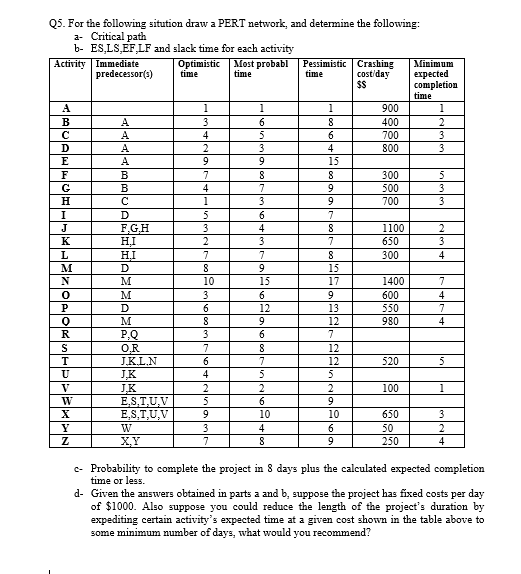
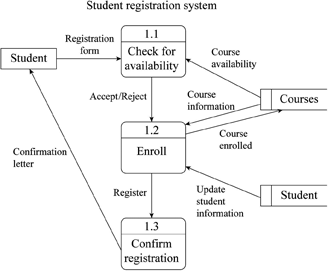
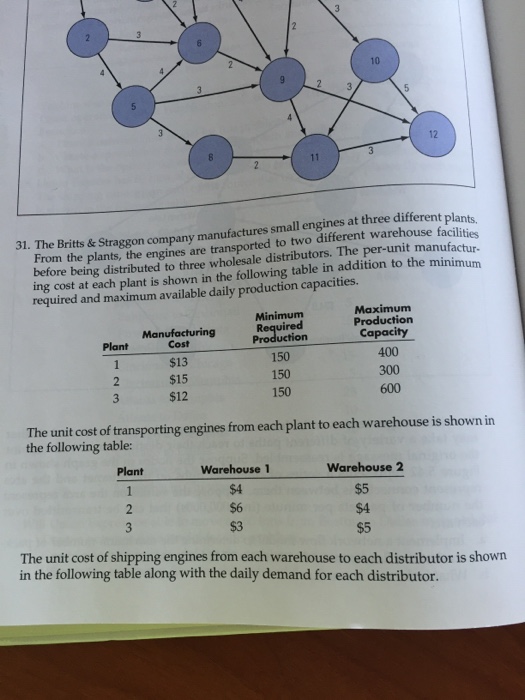
Consider the following Bayesian Belief Network conditional probability table (CPT), and compute answers the following questions: P(B-T) P(B-F) 0.001 0.999 A P(AC-T) P(AC-F) T 0.90 0.10 F 0.05 0.95 Burglary Ali Calls Alarm Earthquake Veli Calls P(E=T) P(E=F) 0.002 0.998 BEP(A=T) P(A=F) TT 0.95 0.05 TF 0.94 0.06 FT 0.29 0.71 FF 0.001 0.999 A P(VC-T) P(VC-F) 0.30 T 0.70 F 0.01 0.99 c) What is the probability that there is a burglary given that Veli calls? d) What is the probability that there is earthquake given that Ali calls? Bayesian Belief Networks: An Example CPT: Conditional Probability Table Bayesian Belief Network Sprinkler Grass wet PRILO FANT F F 044 TON W Rain STAGI SPRINKLER MAIN T F F T 0.01 0.99 COMISIE F Derivation of the probability of a particular n combination of values of X, from CPT: P(x,...,x)= II P(x| Parents(Y;)) i=1 Bayesian Belief Networks: An Example Pr(R-T|G-T) = SPRINT SPRINKLER RANT F F 0.4 0.6 T 0.00 0.99 SMINKLER MAT I 23 10 02 23 01 GRASSWET F T T BAN GRASS WET SPRINKLER FANT F SPRINKLER F 0.0 1.0 T The joint probability function: Pr(G, S, R) = Pr(G | S, R) Pr(S | R) Pr(R) The model can answer the question like: what is the probability that it is raining, given the grass is wet? The corresponding conditional probability function: GMASSWET 0.8 0.2 T 0.59 0.00 shows the conditional probability for each possible combination of its parents F 0.9 T 0.99 0.01 GRASS WET SPRINKLER KAN T F F T Pr(G=T, R=T) Esarr Pr(G-T, S.R=T') Pr(GT) s,Rr.F) Pr(G=T, S, R) Bayesian Belief Networks: An Example PAIN 1.0 F0.0 T 0.8 0.2 MAIN T F 0.2 48 MAIN T F 0.2 08 Let's calculate the conditional probability: = Pr(R =T | G=T) - Pr(G-T,R=T) Estr. Pr(G=T, S, R=T) ERIT.F) Pr(G-T, S, R) Pr(G-T) Next we need to calculate: Pr(G= T) which is a sum of 4 probabilities 0.0019877 0.15847 891 Finally: Pr(RT | G=T) = 0.00198TTT +0.288TTF +0.1584TFT +0.0TFF 2491 Pr(GT,ST, R = T) = Pr(G = T| S=T,R=T) Pr(S =T | R = T) Pr(R = T) = 0.99 0.01 x 0.2 = 0.00198. Now we need to do this: Pr(G = T, S = F, R= T) 35.77%. 2. Suppose each random variable takes three states, i.e., A can take values in {ao, a1,92), B can take values in {bo, b,b2} and so on. What is the minimum number of parameters to exactly express the above model, i.e., to express the joint distributions p(A, B, C, D, E, F) (2.5 marks)? Please also justify your answer (2.5 marks). (In total 5 marks) 3. Check whether the following statements are true. If you think the statements are true, then type T, otherwise type F. Please just type five characters for the five questions in order. For example, if you think the first four are true and the last is false, then simply type TTTTF. We also need you to justify your answer in the last bullet. A and B are independent (0.5 mark) -A and B are conditionally independent given D (0.5 mark) A and E are conditionally independent given D (0.5 mark) - E and F are independent (0.5 mark) -E and F are conditionally independent given D (0.5 mark). Use the expression of joint distribution to justify your answer, i.e., either prove the independency or show it does not hold (2.5 marks). Hint: there is no need to consider all random variables in the Bayesian network. 4. Suppose each random variable only takes two states, i.e., A can take values in {ao, a1}, B can take values in {bo, bi and so on. Suppose the (conditional) probability tables of this model are as follows. Please note that this assignment is worth more points than other homework assignments, because more is expected. This homework assignment can only be successfully completed by drawing upon knowledge gained throughout the semester. For this homework, students will design a networking solution for a fictional company (Wichita Boat, Inc). This will require that the infrastructure be upgraded and expanded in a manner that produces an efficient, secure, reliable, solution. The solution should include: A very brief description of the organization A description of the reason(s) behind the IT changes Tradeoffs that were made in selecting the solution A discussion of alternative solutions may be necessary A list and description of requirements for the implementation Implementation requires more than just IT products. A detailed description of the design This needs to include illustrations of the network design of the solution. THE FICTIONAL COMPANY Wichita Boat, Inc. Wichita Boat, Inc. is expanding and has asked for your help with their IT problems. You have met with the company president and learned the following information. Wichita Boat, Inc. is located in Wichita, where it has office space and a manufacturing plant. The plant has some large equipment. The office has 50 users and the plant has 35 users. The infrastructure consists of an aging file server, an old application server, 45 desktop computers, and two networked laser printers on a 10base-T local area network. The servers are housed in a room that stores janitorial equipment and supplies. The network electronics consist of one 24-port switch and two 20-port hubs. Internet access does not exist. The server currently hosts about 45GB of data. Management estimates that another 275GB of data will be created over the next five years. The current users have some problems that they want fixed during this expansion. First, those who travel want access to the company network and its information systems when they are away from the office. Second, upper management has no privacy when printing and receiving faxes. And third, the employees on the shop floor have made numerous complaints about the accounting system. They report that MS Office seems to work alright, but that the accounting system routinely disappears. Part of the expansion will be local. Thirty-five office employees and 24 plant workers will be added. Each of the new office employees will need a computer, whereas only half of the new plant workers will need a computer. The company wile unused space in its current building. The company also wants a web site to advertise its products, support its customers, and sell accessories. The stipulation has been made that the web presence must not compromise the performance, reliability, or security of the company's network. Wichita Boat, Inc. has just purchased a supplier that's located in River Falls, WI. The River Falls office will remain in its present location. The former supplier's network will need to connect to the Wichita network so that users at both sites can share files and email messages. The users at the former supplier's office will also need to use the accounting application that is located in Wichita. A small office will be setup in Banjarmasin, Indonesia for about one year. The members of this office will research local boat-building techniques and investigate purchasing local lumber. This office will have three employees. One employee will remain at the office, while the other two are expected to spend most of their time out of the office. Q5. For the following sitution draw a PERT network, and determine the following: a- Critical path b- ES,LS,EF LF and slack time for each activity Activity Immediate B C D E F G H I J K L M N 0 P 0 R S T U W X Z predecessor(s) A A A A B B D F,G,H H.I H.I D M M D M P,Q O.R J.K.L.N J,K J.K E,S,T,U,V E,S,T,U,V W X,Y Optimistic time 1 3 4 2 9 7 4 1 5 3 2 7 8 10 3 6 8 3 7 6 4 2 5 9 3 7 Most probabl time 1 6 5 3 9 8 7 3 6 4 3 7 9 15 6 12 9 6 8 7 5 2 6 10 4 8 Pessimistic Crashing time cost/day $$ 1 8 6 4 15 8 9 9 7 8 7 8 15 17 9 13 12 7 12 12 5 2 9 10 6 9 900 400 700 800 300 500 700 1100 650 300 1400 600 550 980 520 100 650 50 250 Minimum expected completion time 1 2 3 3 5 3 3 2 3 4 7 4 7 4 5 1 3 2 4 - Probability to complete the project in 8 days plus the calculated expected completion time or less. d- Given the answers obtained in parts a and b, suppose the project has fixed costs per day of $1000. Also suppose you could reduce the length of the project's duration by expediting certain activity's expected time at a given cost shown in the table above to some minimum number of days, what would you recommend? Student Student registration system Registration form Confirmation letter 1.1 Check for availability Accept/Reject 1.2 Enroll Register 1.3 Confirm registration Course availability Course information Course enrolled Update student information Courses Student Plant 1 2 3 Manufacturing Cost 2 $13 $15 $12 Plant 1 2 3 2 31. The Britts & Straggon company manufactures small engines at three different plants. From the plants, the engines are transported to two different warehouse facilities before being distributed to three wholesale distributors. The per-unit manufactur- ing cost at each plant is shown in the following table in addition to the minimum required and maximum available daily production capacities. Minimum Required Production 2 150 150 150 Warehouse 1 $4 $6 $3 11 3 3 10 Maximum Production Capacity 400 300 600 The unit cost of transporting engines from each plant to each warehouse is shown in the following table: 12 Warehouse 2 $5 $4 $5 The unit cost of shipping engines from each warehouse to each distributor is shown in the following table along with the daily demand for each distributor.