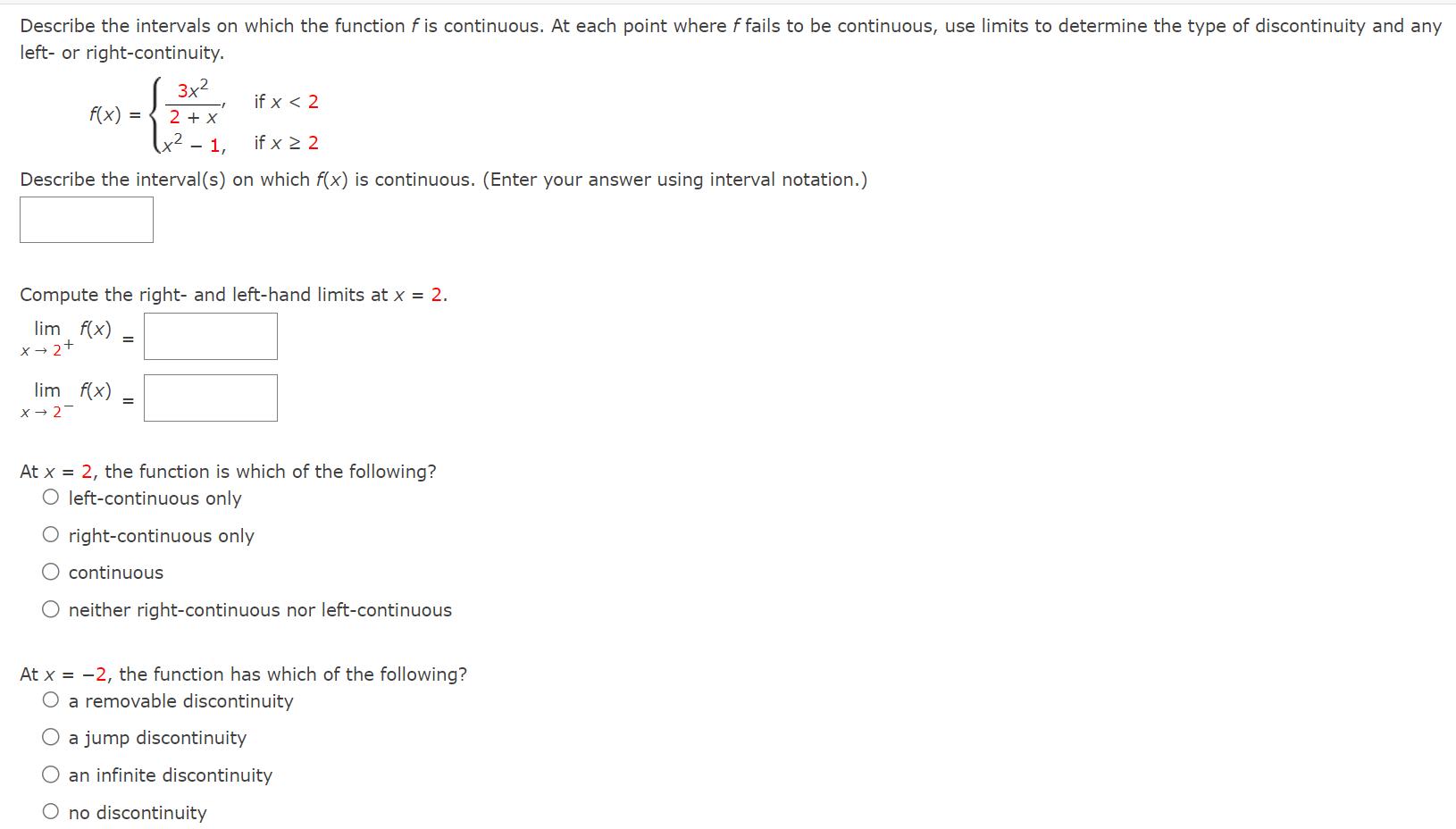
Describe the intervals on which the function f is continuous. At each point where f fails to be continuous, use limits to determine the type of discontinuity and any left or right-continuity. 3x if x < 2 f(x) = 2 + x 2 - 1, if x 2 Describe the interval(s) on which f(x) is continuous. (Enter your answer using interval notation.) Compute the right- and left-hand limits at x = 2. lim f(x) = x 2+ lim f(x) = X-2- At x = 2, the function is which of the following? O left-continuous only O right-continuous only O continuous O neither right-continuous nor left-continuous At x = -2, the function has which of the following? O a removable discontinuity a jump discontinuity an infinite discontinuity O no discontinuity