First three pages are the same question, following 9 pages are equations can use only. No acceleration

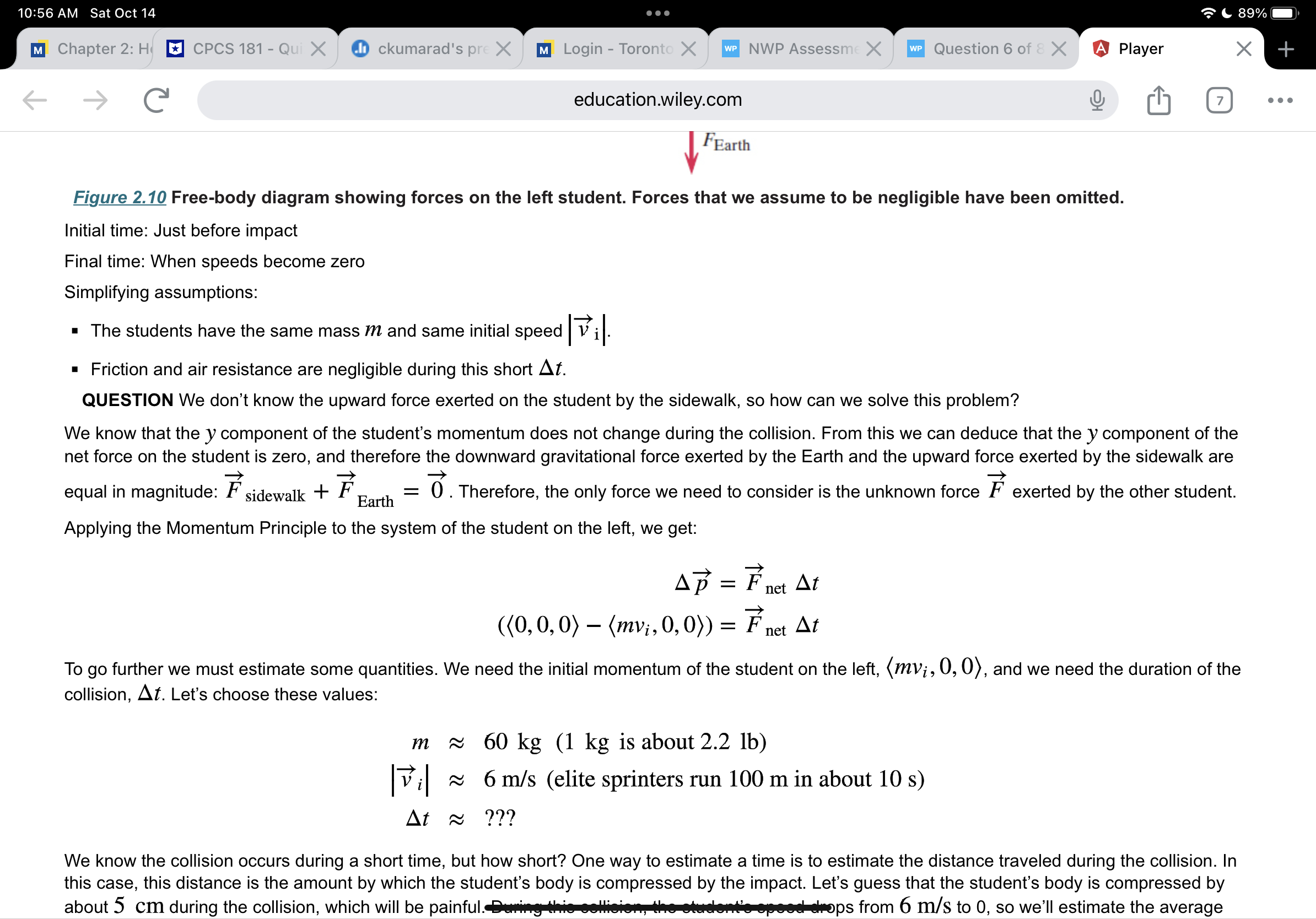
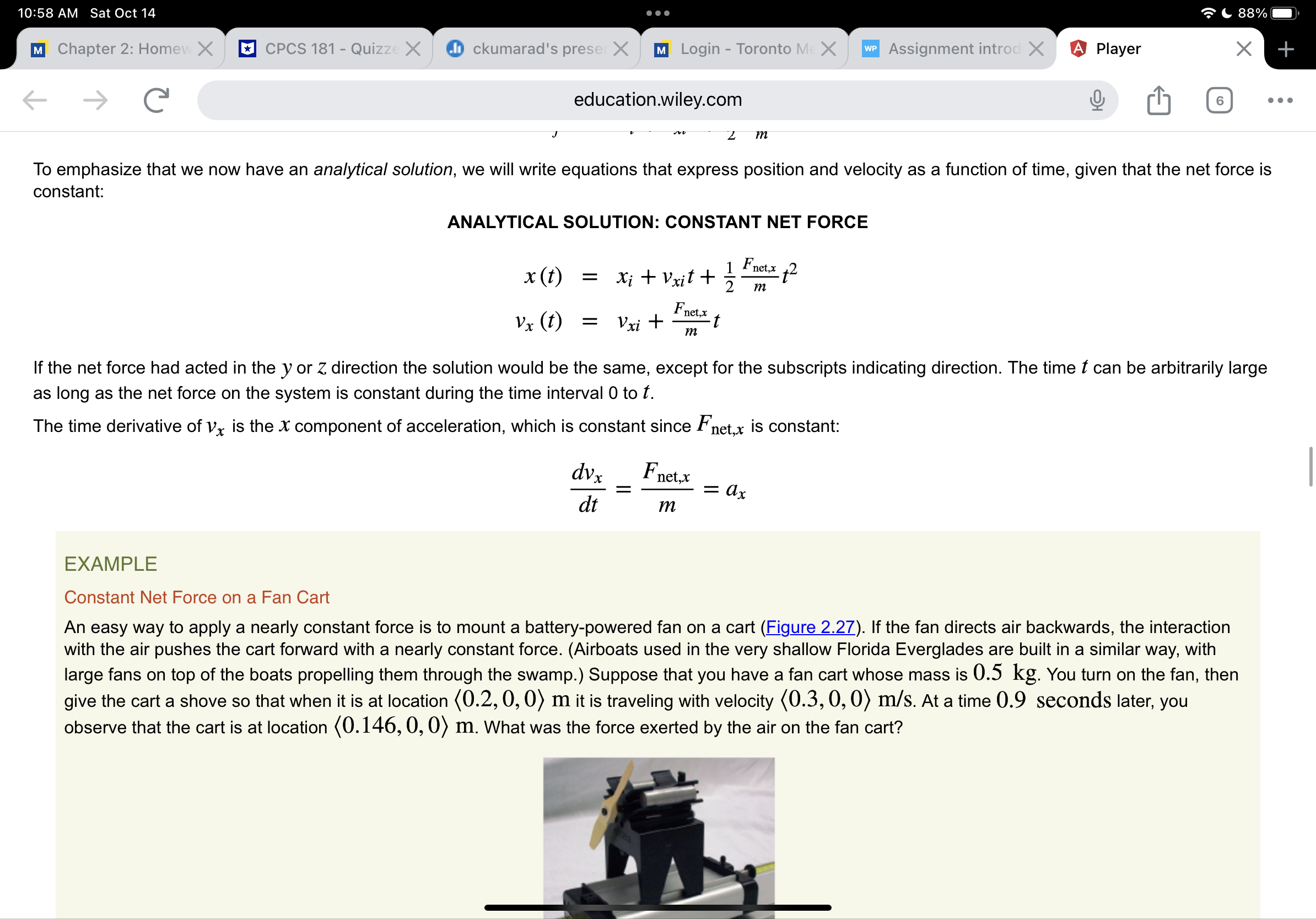
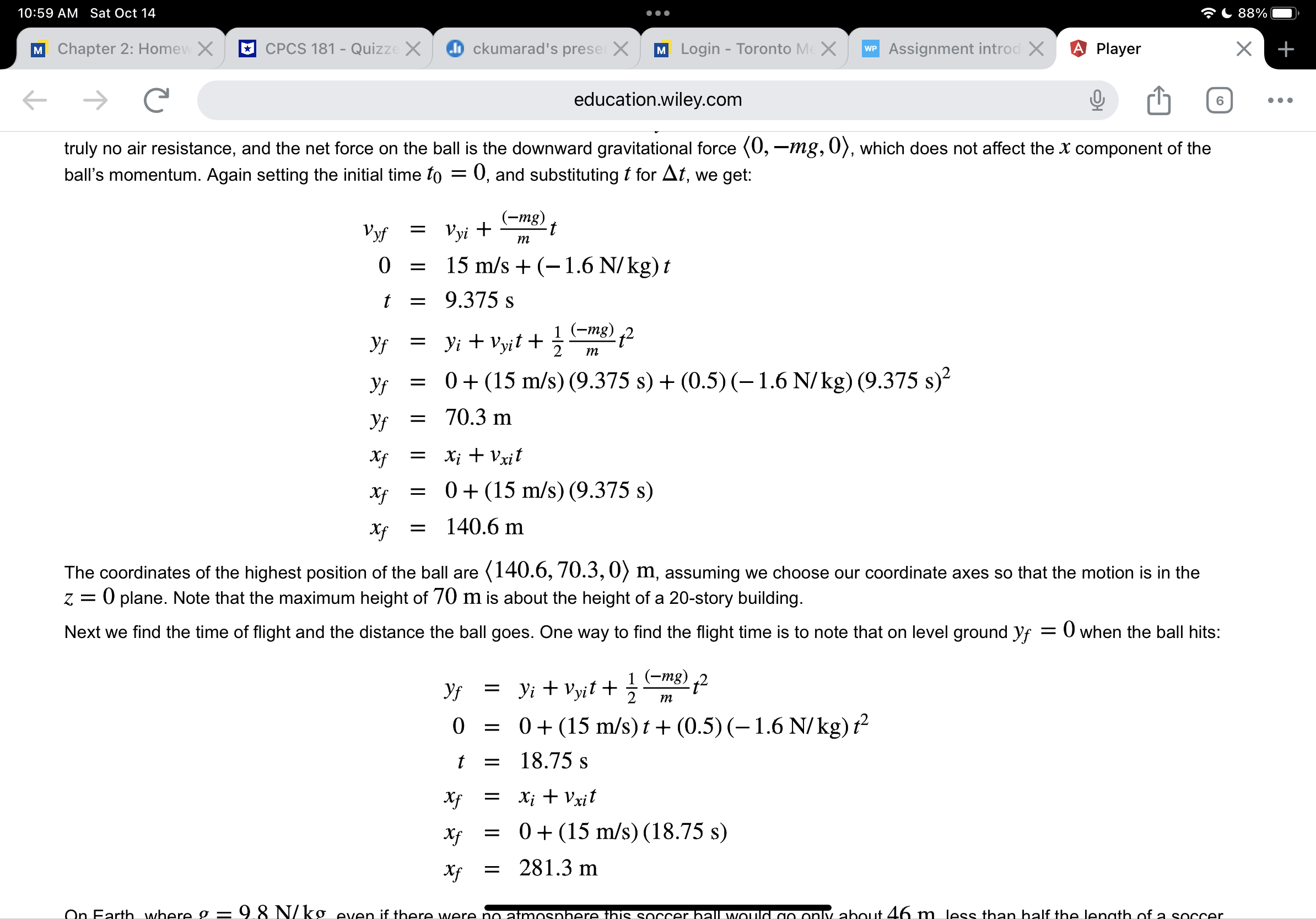
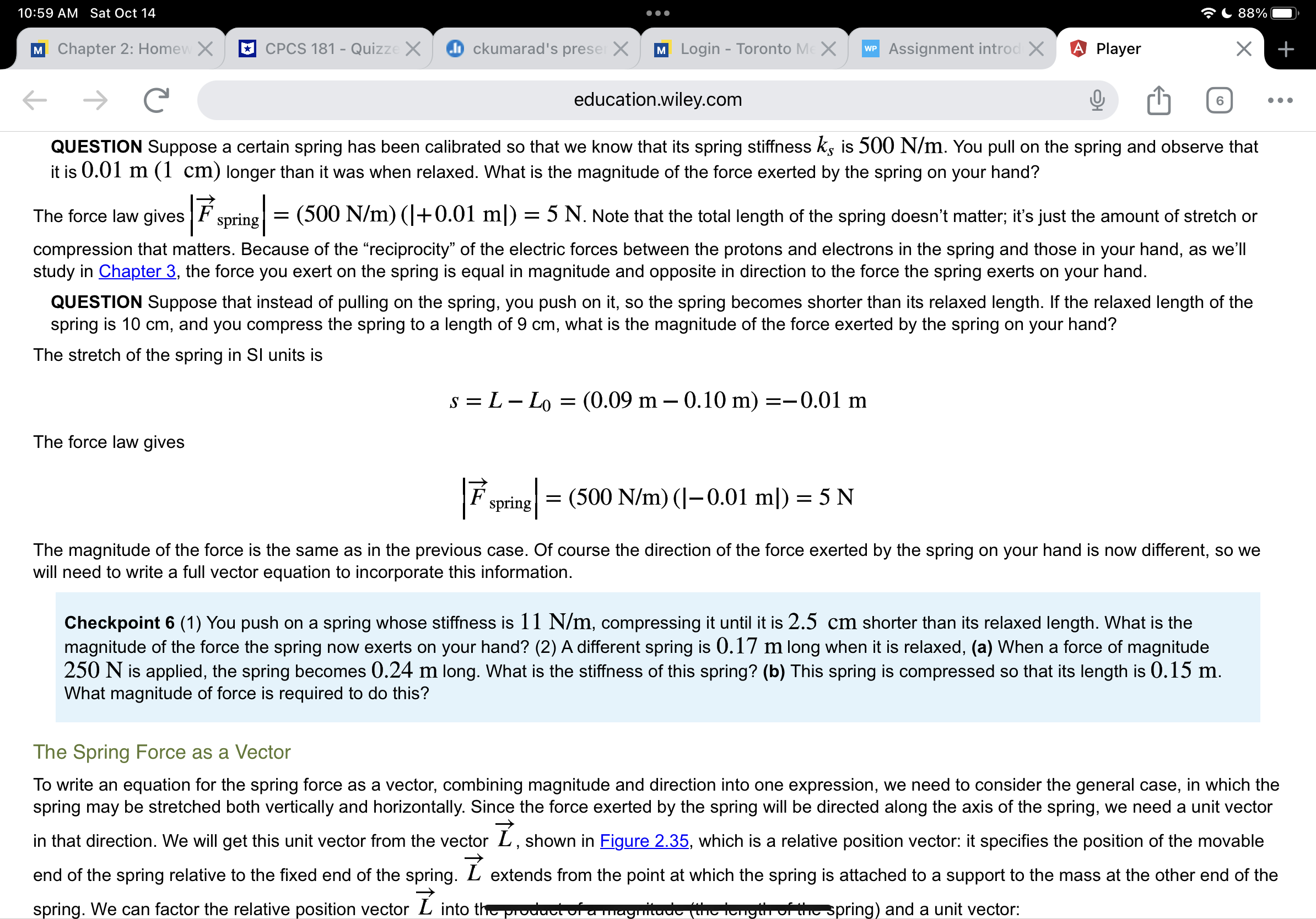
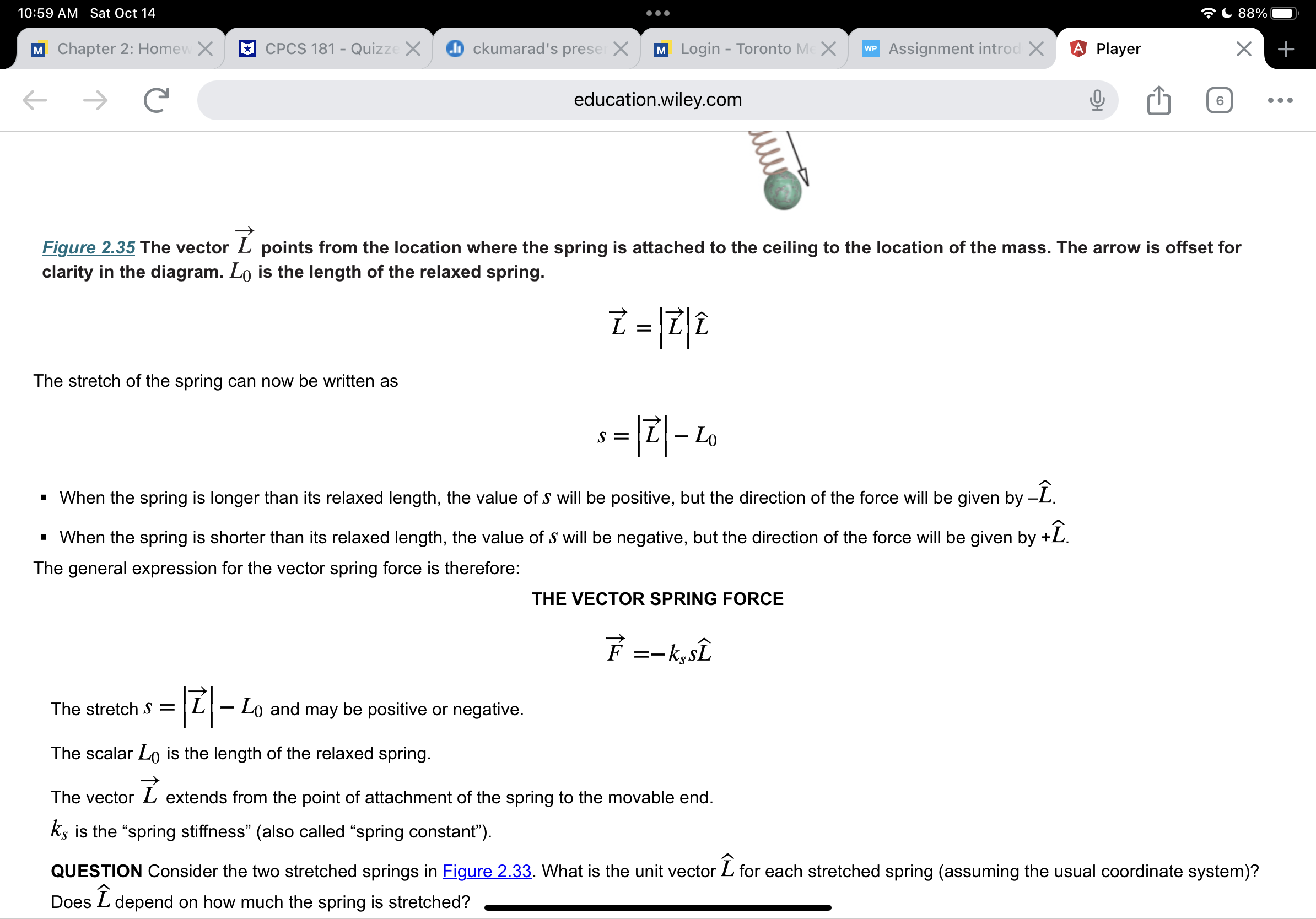
Question 6 of8 10/ 10 E Atennis ball has a mass of 0.057 kg. A professional tennis player hits the ball hard enough to give it a speed of 47 m/s (about 105 miles per hour.) The ball moves toward the left, hits a wall and bounces straight back to the right with almost the same speed (47 m/s). As indicated in the diagram below, high-speed photography shows that the ball is crushed about d = 2.0 cm at the instant when its speed is momentarily zero, before rebounding. Making the very rough approximation that the large force that the wall exerts on the ball is approximately constant during contact, determine the approximate magnitude of this force. Part 1 Your Answer Correct Answer V Your answer is correct. (a) What is the average speed of the ball during the period from rst contact with the wall to the moment the ball's speed is momentarily zero? w = Attempts: 1 of 4 used Part 2 Your Answer Correct Answer V Your answer is correct. 10:56 AM Sat Oct 14 . . . 89% education.wiley.com 10/ 10 E 5 Part 3 YourAnswer Correct Answer V Your answer is correct. (c) What is the magnitude of the average force exerted by the wall on the ball during contact? ) I F avg : N Attempts: 1 of 4 used Part 4 Your Answer Correct Answer V Your answer is correct. (d) In contrast, what is the magnitude of the gravitational force of the Earth on the ball? mg = N eTextbook and Media Attempts: 1 of 4 used 10:56 AM SatOcti4 '.~'& 89%- m Chapter 2: F CPCS I81 I O ckumarad's \"1 Login Tore NWP Assess Question 6 ( G education.wiley.com Q [I] . . . trliurth gure 2.10 Free-body diagram showing forces on the left student. Forces that we assume to be negligible have been omitted. Initial time: Just before impact Final time: When speeds become zero Simplifying assumptions: _) - The students have the same mass m and same initial speed I 12 3|. - Friction and air resistance are negligible during this short At. QUESTION We don't know the upward force exerted on the student by the sidewalk, so how can we solve this problem? We know that the y component of the student's momentum does not change during the collision. From this we can deduce that the y component of the net force on the student is zero, and therefore the downward gravitational force exerted by the Earth and the upward force exerted by the sidewalk are > > > equal in magnitude: Fsidewalk + FE ] = 0 . Therefore, the only force we need to consider is the unknown force F exerted by the other student. Applying the Momentum Principle to the system of the student on the left, we get: A? : Fnet Al (i' O ckumarad's \"1 Login Toro NWP Assess Question 6 ( G education.wiley.com Q [I] . . . We know the collision occurs during a short time, but how short? One way to estimate a time is to estimate the distance traveled during the collision. In this case, this distance is the amount by which the student's body is compressed by the impact. Let's guess that the student's body is compressed by about 5 cm during the collision, which will be painful. During this collision, the student's speed drops from 6 m/s to 0, so we'll estimate the average speed as the \"arithmetic average" (6 In/S + 0 III/S)/2 = 3 III/S (more about this later in the chapter). All motion is in the x direction, so: Ax = vavgJAt 0.05 m z 3 m/s At At 2: 0.017 s The whole interaction lasts only about 0.02 S! The force exerted by one student on the other must be very large. Let's see about how large it is: ( Fm, z (21100, 0, 0) N Check: - The units check (N ' S = kg - m/S, so (kg ' m/S)/S = N). - Is the result reasonable? 21,000 N is a very large force. As we will see in Section 2.4, the gravitational force on a 60 kg student (the \"weight") is only about 600 N. The force of the impact is about 35 times the weight of the student! It's like having a stack of 35 students sitting on you. If the students hit heads instead of stomachs, the squeeze might be less than 1 cm, and the force would be over 5 times as large! This is why heads can break in such a collision. Our result of 21,000 N shows why collisions are so dangerous, Collisions involve very large forces acting for very short times, giving impulses of ordinary magnitude. QUESTION Estimating masses or distances is usually not difficult, but most people find it more challenging to estimate time durations, especially if the times are very short. Why would a guess of 1 second for At have been a poor guess? At an average speed of 3 m/s, each student would have traveled 3 meters during a onesecond impact. This is clearly not physically possiblethey would have had to pass through each other to do this! 10:58 AM Sat Oct 14 88% M Chapter 2: Homew X CPCS 181 - Quizze X ckumarad's prese X MI Login - Toronto Me X WP Assignment introd X A Player X + -> education.wiley.com 6 . . . In contrast to an iterative solution, an analytical solution to a problem yields a mathematical function that gives the value of a quantity of interest as a function of time. If such a function exists, one can use it to find the position or velocity of a system at a given time in one step, instead of taking many small steps to get this information. It is not always possible to get an analytical solution, so iterative methods are of more general applicability. One case in which an iterative solution is possible is the case of constant net force. We will derive this analytical solution to illustrate the approach and the nature of the results. Approximations for Average Velocity In the previous iterative solution for the motion of a tennis ball, we used the approximation P future ~ Vfuture ~ Wave m for the average velocity over each time interval At. QUESTION Why didn't we calculate the average velocity directly from the definition? We can't calculate the average velocity directly from the definition AT V avg = At At because the final location I f of the moving ball is unknown. Since we do not have any other information that would allow us to determine the average velocity, we need to find an approximate value for the average velocity in this situation. There are two possible approaches: (1) If the change in velocity is small over the time interval of interest, we can use the final velocity (or the initial velocity) as an approximation to the average velocity. (2) Alternatively, we can average two values of velocity to approximate the average velocity. QUESTION What might be a better approximation for V avg if the net force on a system is constant? Let's consider using the arithmetic average: Vavg ~ V future + V now 2 The arithmetic average lies between the two values. For example, the arithmetic average of 6 and 8 is (6 + 8)/2 = 14/2 = 7, halfway between 6 and 8. The10:58 AM Sat Oct 14 88% M Chapter 2: Homew X CPCS 181 - Quizze X ckumarad's prese X M] Login - Toronto Mc X We Assignment introd X A Player X education.wiley.com 6 . . . Vavg,x = = 44 mi /h 5 h APPROXIMATE AVERAGE VELOCITY Vavg~ V future + V now 2 This is exactly correct if all components of 1 change linearly with time (acceleration is constant). However, it may be a poor approximation if the net force is not constant. Analytical Solution for Constant Net Force The term analytical describes a solution that can be written symbolically (algebraically). In many cases it is not possible to find an analytical solution for the motion of a system. However, if the net force on a system is constant, we can easily find an analytical solution of the form r (t) = .... Consider a system on which there is a constant net force in the + x direction during the time At. For ordinary speeds y ~ 1, so Vx ~Px/m. Using (a) the Momentum Principle in its update form, (b) the position update equation, and (c) the special result for average velocity in the case of constant net force, we can easily derive equations for the position and velocity as a function of time. For convenience we'll start measuring the time f from 0, and write t to represent At: Pxf = Pxi + Fnet,xt Vxf = Vxi+ Fnet,x m (vxit -netz t ) + Vxi Vavg,x 2 1 Fnet,x + Vavg,x = Vxi + 2 m Xf = xi + Vavg,xt Xf = xit Vxit+? 1 Fnet,x +2 m To emphasize that we now have an analytical solution, we will write equations that express position and velocity as a function of time, given that the net force is10:58 AM SatOctl4 '.~'& 88%- m Chapter 2: Her CPCS 181 Qu' O ckumarad's prv m Login Torontt Assignment int G education.wiley.com Q [I] . . . J ,. A L m To emphasize that we now have an analytical solution, we will write equations that express position and velocity as a function of time, given that the net force is constant: ANALYTICAL SOLUTION: CONSTANT NET FORCE F116 x(t) = xi+vxit+% m\"? Fnex vx(t) = vxi+ \"ft If the net force had acted in the y or Z direction the solution would be the same, except for the subscripts indicating direction. The time t can be arbitrarily large as long as the net force on the system is constant during the time interval 0 to t. The time derivative of v, is the )6 component of acceleration, which is constant since F113,; is constant: dvx Fnct,x dt m 2a)., EXAMPLE Constant Net Force on a Fan Cart An easy way to apply a nearly constant force is to mount a battery-powered fan on a cart (gure 2.27). If the fan directs air backwards, the interaction with the air pushes the cart forward with a nearly constant force. (Airboats used in the very shallow Florida Everglades are built in a similar way, with large fans on top of the boats propelling them through the swamp.) Suppose that you have a fan cart whose mass is 0.5 kg. You turn on the fan, then give the cart a shove so that when it is at location (0.2, 0, 0) m it is traveling with velocity (0.3, 0, 0) III/S. At a time 0.9 seconds later, you observe that the cart is at location (0.146, 0, 0) In. What was the force exerted by the air on the fan cart? 10:59 AM Sat Oct 14 88% M Chapter 2: Homew X CPCS 181 - Quizze X ckumarad's prese X MI Login - Toronto Mc X We Assignment introd X A Player X education.wiley.com 6 . . . truly no air resistance, and the net force on the ball is the downward gravitational force (0, -mg, 0), which does not affect the x component of the ball's momentum. Again setting the initial time to = 0, and substituting t for At, we get: Vyf = Vyitm8+ m 0 = 15 m/s + (-1.6 N/kg) t t = 9.375 s yf = yi + Vyit+ 15mg)+2 m yf = 0+ (15 m/s) (9.375 s) + (0.5) (-1.6 N/kg) (9.375 s)2 yf = 70.3 m Xf = xi+ Vxit = 0 + (15 m/s) (9.375 s) Xf = 140.6 m The coordinates of the highest position of the ball are ( 140.6, 70.3, 0) m, assuming we choose our coordinate axes so that the motion is in the Z = 0 plane. Note that the maximum height of 70 m is about the height of a 20-story building Next we find the time of flight and the distance the ball goes. One way to find the flight time is to note that on level ground yf = 0 when the ball hits: Yf = yi + Vyit+ 1 Cm8)+2 m 0 = 0+ (15 m/s) t + (0.5) (-1.6 N/kg) 2 t = 18.75 s Xf = xi + Vxit Xf = 0+ (15 m/s) (18.75 s) Xf = 281.3 m :9 8N/ko10:59 AM Sat Oct 14 88% M Chapter 2: Homew X CPCS 181 - Quizze X ckumarad's prese X MI Login - Toronto Me X WP Assignment introd X A Player X + education.wiley.com 6 . . . amount of stretch or compression of the spring. The force is directed along the line of the spring. The Spring Force A "force law" describes mathematically how a force depends on the situation. For a spring, it is determined experimentally that the force exerted by a spring on an object attached to the spring is given by the following equation: MAGNITUDE OF THE SPRING FORCE F spring = Ks Is| Is | is the absolute value of the stretch: s = L - Lo. Lo is the length of the relaxed spring. L is the length of the spring when stretched or compressed. ks is the "spring stiffness" (also called "spring constant"). The force acts in a direction to restore the spring to its relaxed length. The constant ks is a positive number, and is a property of the particular spring: the stiffer the spring, the larger the spring stiffness, and the larger the force needed to stretch the spring. Note that S is positive if the spring is stretched (L > Lo, Figure 2.33) and negative if the spring is compressed (L in that direction. We will get this unit vector from the vector L, shown in gure 2.35, which is a relative position vector: it specifies the position of the movable _) end of the spring relative to the fixed end of the spring. L extends from the point at which the spring is attached to a support to the mass at the other end of the _) spring. We can factor the relative position vector L into tWWpring) and a unit vector: 10:59 AM SatOctl4 ' 'sc 88%- m Chapter 2: H01 CPCS 181 Qu' O ckumarad's pr' m Login Torontr Assignment int G education.wiley.com Q [I] . . . gure 2.35 The vector L points from the location where the spring is attached to the ceiling to the location of the mass. The arrow is offset for clarity in the diagram. L0 is the length of the relaxed spring. > > A L = IL I L The stretch of the spring can now be written as a s = |L| L0 I When the spring is longer than its relaxed length, the value ofs will be positive, but the direction of the force will be given by L. - When the spring is shorter than its relaxed length, the value of S will be negative, but the direction of the force will be given by +L. The general expression for the vector spring force is therefore: THE VECTOR SPRING FORCE ) A F =kssL _, The stretch S = ILI L0 and may be positive or negative. The scalarLo is the length of the relaxed spring. _) The vector L extends from the point of attachment of the spring to the movable end. ks is the \"spring stiffness\" (also called \"spring constant"). QUESTION Consider the two stretched springs in gure 2.33. What is the unit vector L for each stretched spring (assuming the usual coordinate system)? Does L depend on how much the spring is stretched