Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Full Model Ridge Regression Ridge Regression (Intercept) 116.3 119.3 158.5 Age 1.1 1.0 0.3 Asthma 0.7 0.5 0.4 CAD 17.0 16.9 10.0 CHF 8.0 8.6
| Full Model | Ridge Regression | Ridge Regression | |
|---|---|---|---|
| (Intercept) | 116.3 | 119.3 | 158.5 |
| Age | 1.1 | 1.0 | 0.3 |
| Asthma | 0.7 | 0.5 | 0.4 |
| CAD | 17.0 | 16.9 | 10.0 |
| CHF | 8.0 | 8.6 | 9.4 |
| CKD | 19.5 | 19.8 | 12.8 |
| COPD | -5.4 | -4.0 | 4.5 |
| Depression | 31.1 | 29.9 | 10.3 |
| Diabetes | 11.0 | 10.9 | 6.9 |
| ESRD | 31.1 | 29.3 | 11.3 |
| Female | -2.5 | -2.1 | 0.2 |
| HIV | 70.7 | 68.2 | 23.2 |
| Hyperlipidemia | 19.9 | 19.5 | 10.2 |
| Hypertension | -8.2 | -5.5 | 5.8 |
| Injury | -23.6 | -22.2 | -5.9 |
| Obesity | 8.9 | 8.7 | 6.0 |
| Substance_Abuse | 40.2 | 38.2 | 10.5 |
| Wait_Time | 0.7 | 0.7 | 0.2 |
| RMSE - Ridge Regression, |
|---|
| 120.57 |
To compute the test error for the ridge.min model,
- compute the predicted values of the response by applying the ridge.min estimated above to the test_set
x=model.matrix(LOV~ .,data = test_set)[,-1] predicted=predict(ridge.min,newx=x)
- compare the observed values of the response in the test set, test_set$LOV, to the predicted values of the response obtained in step 1 (for reference below save the result as rmse_ridge.min)
rmse_ridge.min=round(rmse(test_set$LOV, predicted),2) knitr::kable(rmse_ridge.min, col.names =c("RMSE -- Ridge Regression, $\\lambda_{min}$"))
RMSE - Ridge Regression, 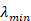 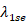 |
|---|
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


