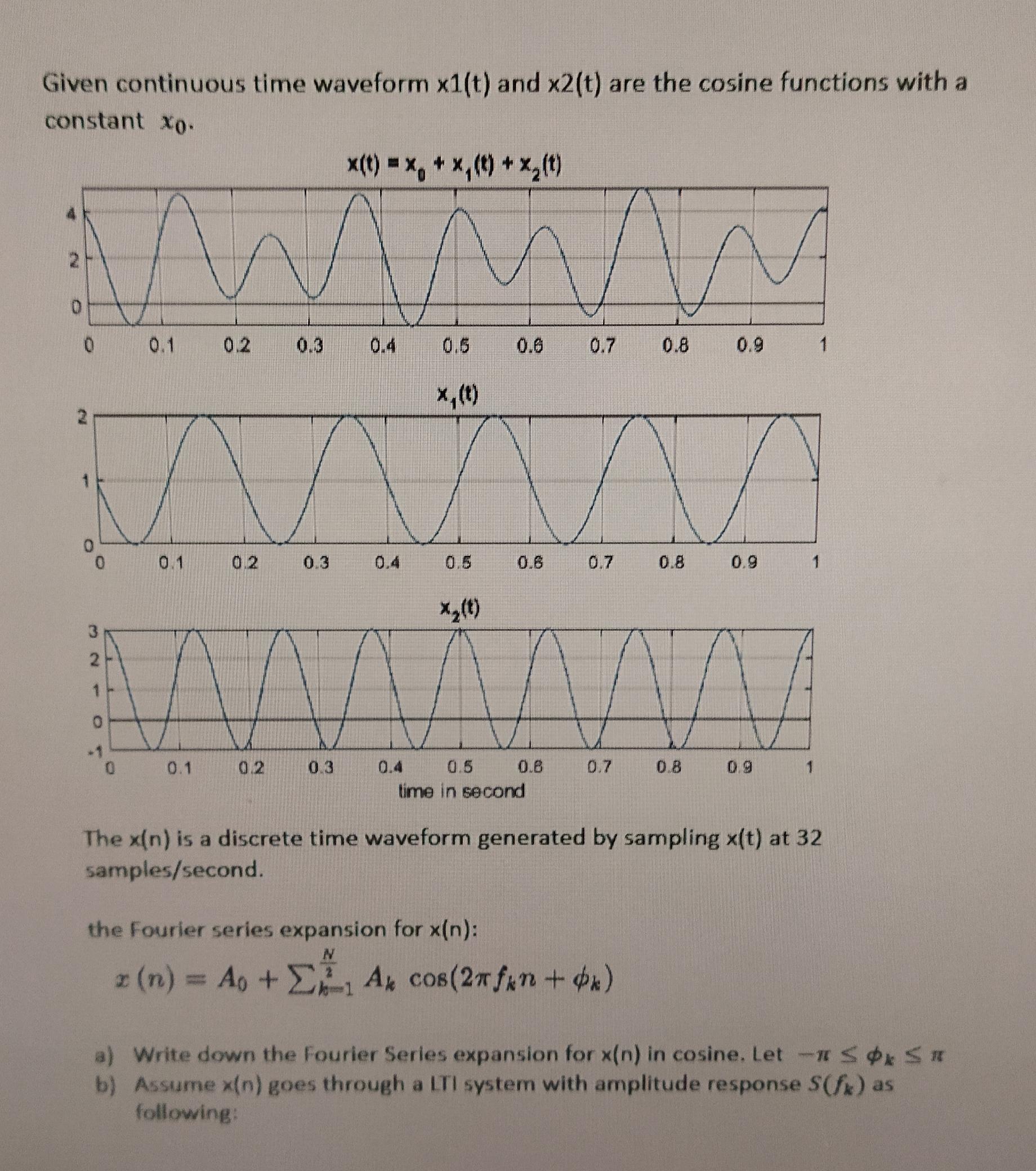
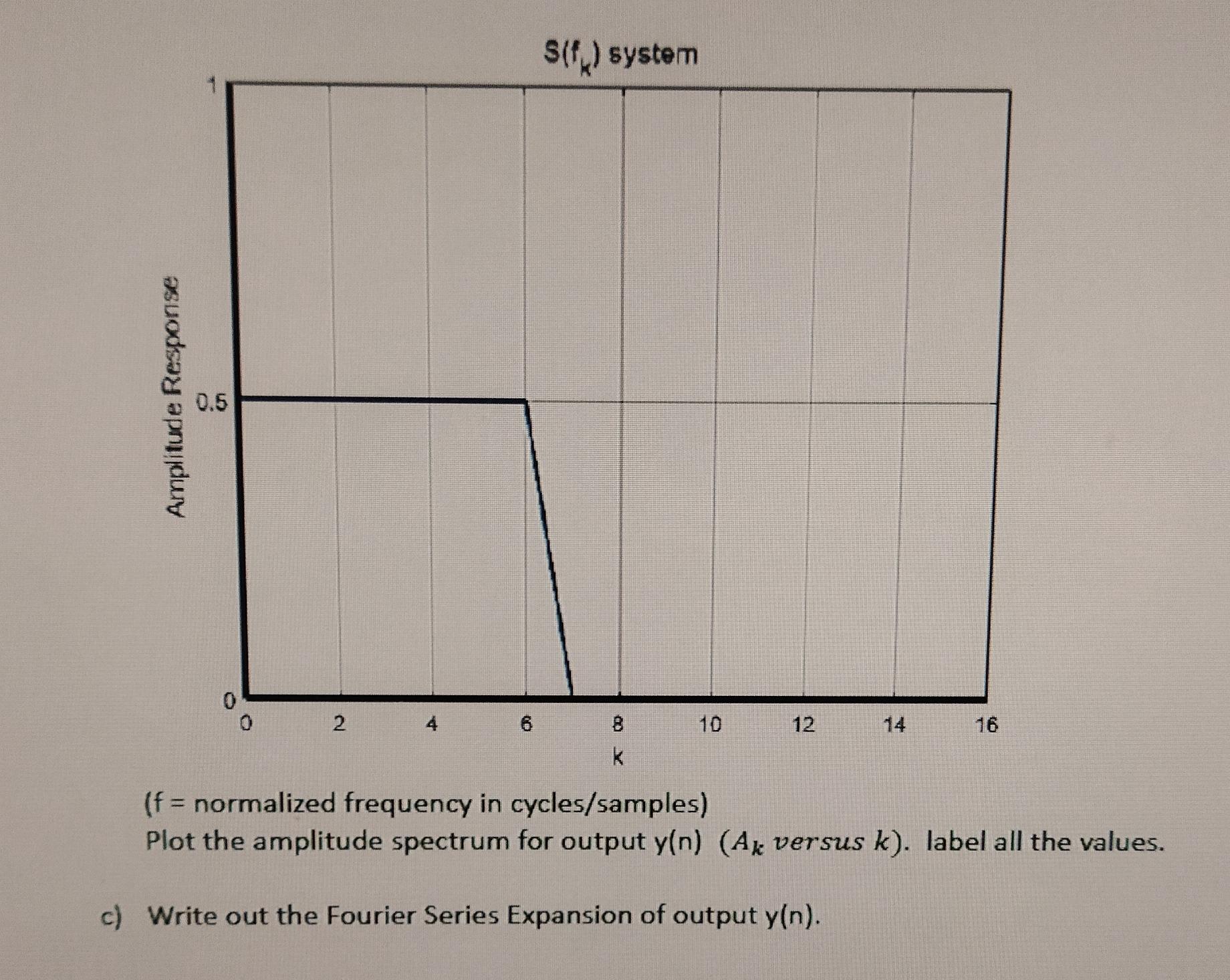
Given continuous time waveform x1(t) and x2(t) are the cosine functions with a constant Xo. x(t) = x, + x,() + x,(t) 0. 0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0.7 0.4 time in second 0.1 0.2 0.3 0.5 0.8 0.8 0.9 1 The x(n) is a discrete time waveform generated by sampling x(t) at 32 samples/second. the Fourier series expansion for x(n): A, +EA cos(27 fan+x) %3D a) Write down the Fourier Series expansion for x(n) in cosine. Let-nS S b) Assume x(n) goes through a LTI system with amplitude response S(f) as following: 2. 2. 321 O S(f) system 0.5 2 4 6. 8. 10 12 14 16 k (f = normalized frequency in cycles/samples) Plot the amplitude spectrum for output y(n) (A versus k). label all the values. c) Write out the Fourier Series Expansion of output y(n). Amplitude Response