

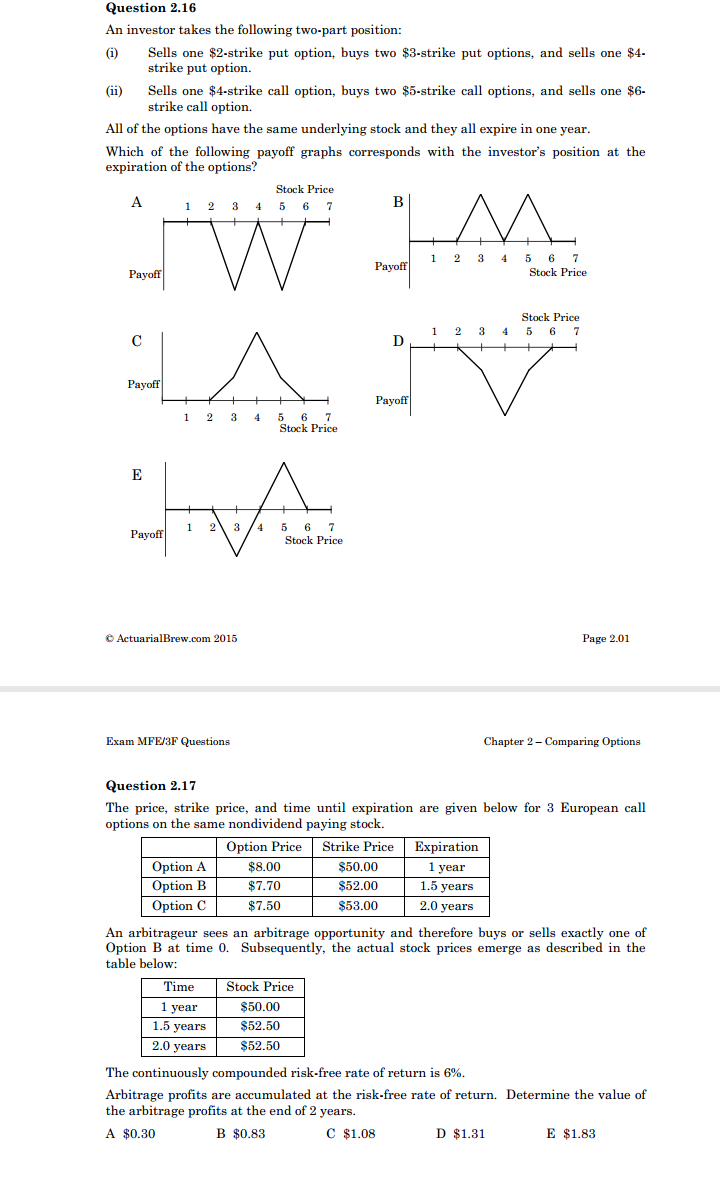


Help me to solve the following
|Consider a market for a homogenous product with four active companies. Firms have a constant marginal cost of production of 510. The market demand is given by Dial = W p- Finns set prices in a repeated game with innite horizon and a discount factor 45 E [13.1]. {a} [12 marks] Construct a subgame perfect equilibrium with trigger strategies in which rms collude on the industry-prot maximising prices and punish deviation by reverting forever to the static Nash equilibrium. Under which condition does this equilibrium hold? {b} [12 marks] Suppose the market demand only arises every second period. In other periods. demand is equal to zero. Construct a subgame perfect equilibrium with trigger strategies in which firms collude on the industry-profit maximising prices and punish deviation by reverting forever to the static Nash equilibrium. Under which condition does this equilibrium hold? {c} [12 marks] Suppose all four firms are active in two markets. Market A is ducn'bed by the setup in sub-question (a). that is. demand arises in everyI period. In the second market. market B. demand only occurs every second period as assumed in subqu-Istion [b]. Construct a subgame perfect equilibrium with trigger strategies in which rms collude on the industry-profit maximising prots and punish deviations by reverting forever to the static Nash equilibrium in both markets. Under which condition does this equilibrium hold\".||I Explain the difference to (a) and {b}. 1. Consider a duopoly market, where two firms sell differentiated products, which are imperfect substitutes. The market can be modelled as a static price competition game. The two firms choose prices p, and pa simultane- ously. The demand functions for the two firms are: Di (p1, p2) = 1+ 2-2 2f and De (p1, p2) = = + 272, where t > 0 measures the degree of product differentiation. Both firms have constant marginal cost c = 0.02 > 0 of production. (a) Derive the Nash equilibrium of this game, including the prices, out- puts and profits of the two firms. (b) From the given demand functions, q = D; (p;, p;) = } + PF2 derive the residual inverse demand functions: p; = Pi(qi, p;) (work out P.(qi, p;)). Show that for t > 0, P(qi, p;) is downward-sloping. i.e.. Dqi 8Pig .Pil c, i.e., firm i has market power. (c) Calculate the limits of the equilibrium prices and profits as t - 0. What is P:(qi, p;) as t - 0? Is it downward sloping? Argue that the Bertrand Paradox (i.e., the prediction of the static Bertrand duopoly model, where pf = p; = c) holds only in the extreme case of t = 0.Question 2.16 An investor takes the following two-part position: (i) Sells one $2-strike put option, buys two $3-strike put options, and sells one $4- strike put option. (ii) Sells one $4-strike call option, buys two $5-strike call options, and sells one $6- strike call option. All of the options have the same underlying stock and they all expire in one year. Which of the following payoff graphs corresponds with the investor's position at the expiration of the options? Stock Price A 2 4 5 6 7 B Payoff 1 2 3 4 5 6 7 Payoff Stock Price Stock Price 2 3 4 5 6 C D Payoff Payoff 1 2 3 4 5 6 Stock Price E 3 /4 Payoff 1 2 5 6 Stock Price ActuarialBrew.com 2015 Page 2.01 Exam MFE/3F Questions Chapter 2- Comparing Options Question 2.17 The price, strike price, and time until expiration are given below for 3 European call options on the same nondividend paying stock. Option Price Strike Price Expiration Option A $8.00 $50.00 year Option B $7.70 $52.00 1.5 years Option C $7.50 $53.00 2.0 years An arbitrageur sees an arbitrage opportunity and therefore buys or sells exactly one of Option B at time 0. Subsequently, the actual stock prices emerge as described in the table below: Time Stock Price 1 year $50.00 1.5 years $52.50 2.0 years $52.50 The continuously compounded risk-free rate of return is 6%. Arbitrage profits are accumulated at the risk-free rate of return. Determine the value of the arbitrage profits at the end of 2 years. A $0.30 B $0.83 C $1.08 D $1.31 E $1.83Question 2.18 Near market closing time on a given day, you lose access to stock prices, but some European call and put prices for a stock are available as follows: Strike Price Call Price Put Price $45 $12 $4 $55 $7 $9 $60 $4 $12 All 6 options have the same expiration date. The risk-free interest rate is zero. After reviewing the information above, Jill tells Sabrina and Kelly that one could use the following zero-cost portfolio to obtain arbitrage profit: Short one put option with strike price 45; long 3 put options with strike price 55; lend $1; and short some number of put options with strike price 60. Sabrina claims that the following zero-cost portfolio can produce arbitrage profit: Long one call option with strike price 45; short 3 call options with strike price 55; lend $1; and long some number of call options with strike price 60. Kelly claims that the following zero-cost portfolio can produce arbitrage profit: Long 2 calls and short 2 puts with strike price 60; long 1 call and short 1 put with strike price 45; lend $2; and short some calls and long the same number of puts with strike price 55. Which of the following statements is correct? A Only Jill is correct. B Only Sabrina is correct. C Only Kelly is correct. D Only Sabrina and Kelly are correct. E None of them is correct. ActuarialBrew.com 2015 Page 2.03 Exam MFE/3F Questions Chapter 2 - Comparing Options Question 2.19 You are given: (i) C(K,T) denotes the current price of a K-strike T-year European call option on a nondividend-paying stock (ii) P(K, T) denotes the current price of a K-strike T-year European put option on the same stock. (iii) S denotes the current price of the stock. (iv) The continuously compounded risk-free interest rate is r, and r > 0. Which of the following is (are) correct? I O S P(85, T) - P(80, T) s 5e-FT II 75e- s P(75,T) - C(80,T) + S s 80e-FT III 80e-TT s P(75, T) - C(80,T) + S s 85 A I only B II only C III only D I and II only E I and III onlyQuestion 2.21] The Following information was known at time D: {i} The continuously compounded risk-tree interest rate is 9%. {ii} The price of a stock is $312]. {iii} The stock pays 2 discrete dividends. {iv} The stock pays a discrete dividend of$2 in 3 months. {v1 The stock pays a second discrete dividend of $1.91] in 9 months. At time I], a 1-year American call option was 1written on the stock. The strike price of the American call option was $33. At time 2, you are informed that the call option did not expire worthless. Determine when the call was exercised. A Time [I E Time 3 months C Time 9 months [J Time 12 months E There is not enough information provided to answer this question. AcmariaIBoewcom 2015 Page 2.114 Exam MFEI'BF Questions Chapter 2 Comparing Uplirme Question 2.21 An insurance company sells single premium deferred annuity contracts with returns linked to a stock index, the time t value of one unit of which is denoted by SE]. The contracts oEl'er a minimum guaranteed return rate of 4%. At time {1, a single premium of P is paid by the policyholder and P x 3% is deducted hy the insurance company. Thus, at the contract maturity date, T, the insurance company will pay the policyholder: SIT] T] 1 M , 1.134 P1: 3%] 3" 0-13[ Si") You are given the iiillowing information: {i} The contract will mature in 2 years. {ii} Dividends are not incorporated in the stock index. That is, the stock index is constructed such that the stock dividends are net reinvested. {iii} The continuously compounded dividend yield of the index is T95 per year. {iv} Sm} = as (v) The price of a 2-year European put option on the index with strike price of $54.03 is $3.96. {vi} The continuously compounded risk-free interest rate is E96. Determine 3% so that the insurance company does not make or lose money on this contract. A 43% E 12% C l.% D 12.2% E 15.2%
















