help please

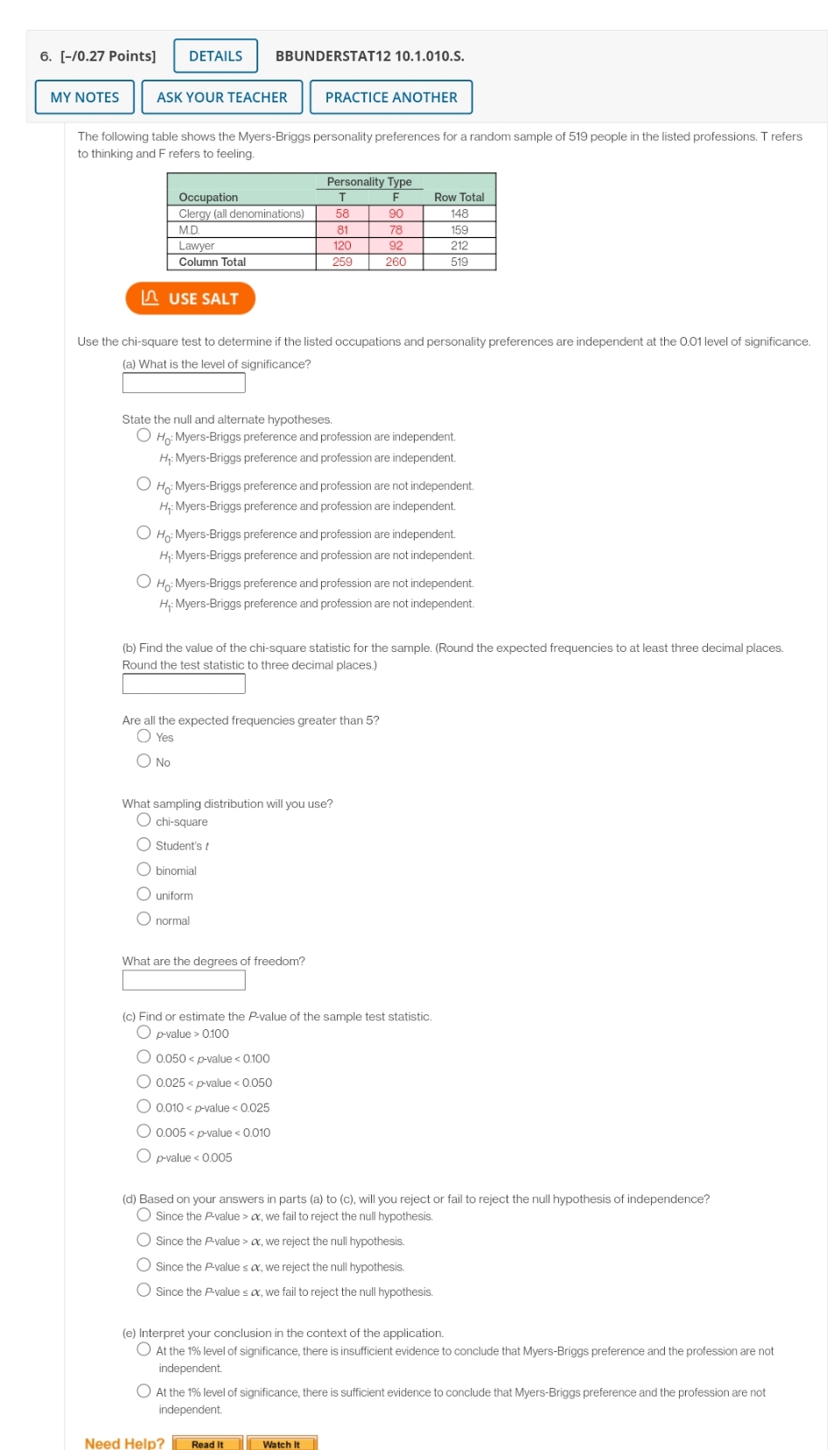
6. [-/0.27 Points] DETAILS BBUNDERSTAT12 10.1.010.S. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER The following table shows the Myers-Briggs personality preferences for a random sample of 519 people in the listed professions. T refers to thinking and F refers to feeling. Personality Type Occupation F Row Total Clergy (all denominations) 58 90 148 M.D 81 78 159 Lawyer 120 92 212 Column Total 259 260 519 LA USE SALT Use the chi-square test to determine if the listed occupations and personality preferences are independent at the 0.01 level of significance. (a) What is the level of significance? State the null and alternate hypotheses. Ho: Myers-Briggs preference and profession are independent. Hy: Myers-Briggs preference and profession are independent. O Ho: Myers-Briggs preference and profession are not independent. Hy: Myers-Briggs preference and profession are independent. O Ho: Myers-Briggs preference and profession are independent. Hy: Myers-Briggs preference and profession are not independent. O Ho: Myers-Briggs preference and profession are not independent. My: Myers-Briggs preference and profession are not independent. (b) Find the value of the chi-square statistic for the sample. (Round the expected frequencies to at least three decimal places. Round the test statistic to three decimal places.) Are all the expected frequencies greater than 5? Yes O No What sampling distribution will you use? O chi-square O Student's t O binomial O uniform O normal What are the degrees of freedom? (c) Find or estimate the P-value of the sample test statistic. O p-value > 0.100 O 0.050 or, we fail to reject the null hypothesis. Since the P-value > ox, we reject the null hypothesis. O Since the P-value s or, we reject the null hypothesis. O Since the P-value s or, we fail to reject the null hypothesis. (e) Interpret your conclusion in the context of the application. At the 1% level of significance, there is insufficient evidence to conclude that Myers-Briggs preference and the profession are not independent At the 1% level of significance, there is sufficient evidence to conclude that Myers-Briggs preference and the profession are not independent