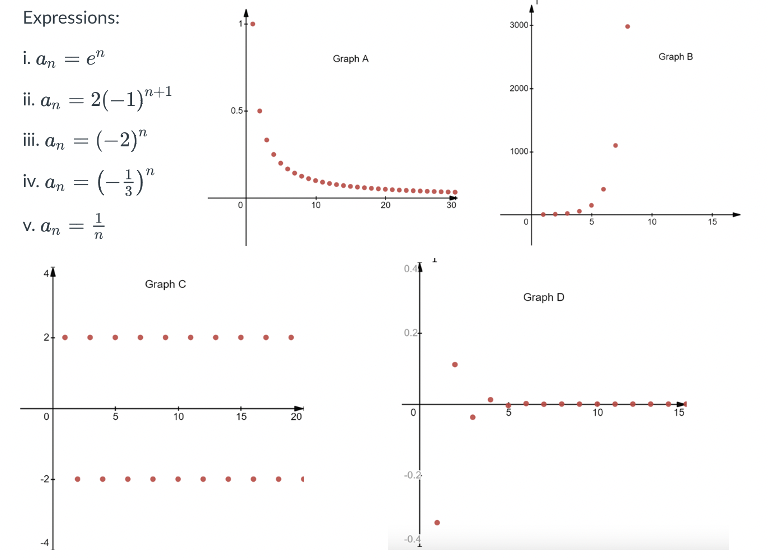
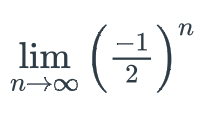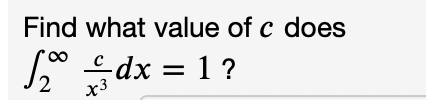I am stuck on these ones. Thanks to whoever is going to help :)

1.

n lim 2 CThe series M (n-1)! converges to the number e. (This is given information. n= 1 You do not need to prove this, but we may be able to prove it before the end of the course.) Compute S1, So, S3, S4, ...... by adding the first several terms of the series. Notice that for each additional term you add, the sum is closer and closer to e. What is the smallest /V such that Sw gives an approximation of the number e that is correct to 3 decimal places? Side note: Some calculators do computations involving e, 7, sin(0.3) and many other transcendental numbers by using sums of series such as the one above (although recently there are also faster methods that calculators can use).DO DO Suppose that _ an and _ by are convergent series and that _ an = 3 n=1 n=1 n=1 and > bn = 5. Also a1 = 1. n=1 Find the sum of each of the following series, or determine that it is divergent, or that not enough information is given. Use Theorem 5.7 as appropriate. 00 a) E (an + bn) n=1 b) E (2an - 3b,) n=1 c) E (an )2 n=1 d) E an n=2a) For the series M8 (-1)" n. compute the 4 th partial sum S4. n=1 b) For the series 2n n+1 compute the 3rd partial sum S3. n=1Each of the following are examples of geometric series. For each one, find a and r and determine whether it converges or diverges. a) For the geometric series _ 5(1)"-1 we see that a = and r = The series is and the sum is b) For the geometric series _ 4($)"-1 we see that a = 4 and T = 1=1 The series is and the sum is c) For the geometric series ) 2- we see that a = and r = The series is and the sum isConsider the integral x21 - 3x14 + 11x7 - 14 dx (x3 - 5x2 + 4x) (x4- 256)2 Enter a T or an F in each answer space below to indicate whether or not a term of the given type occurs in the general form of the complete partial fractions decomposition of the integrand. A1, A2, A3 ... and B1, B2, B3, ... denote constants. You must get all of the answers correct to receive credit. 1. Ayx+By x2+16 2. A7x+B7 (x+4)- 3. Azx+ B2 (x*+256) 4. X-4 5. Bs Y4 6. Ax (a product, not a fraction!) 7. BA (x-1)* 8. B6 x+41. Engineers have observed that when transferring a message I (an input signal] through a physical medium some information is lost in the message 0 that is received (an output signal). Information may be lost due to dissipation as heat is transferredI or for other reasons, depending on physical context. For exampleI when we record music we do not record everything but a finite amount of information. If we represent the input signal by a function Ho). defined for z e [-1r,1r], then one way to measure how much is lost is to compute the percentage loss: 2 If, IKE) - 0($)|2d-'E A IL. more ' where 0(5) represents the output signal. also dened for z E [n,1r]. For example. suppose we are given a transistor that sends an input [(31) to 0(3) = /\" I[t}dt + g (f 1(a) sin(t)dt) sin(..~:}. (a) What is the percentage loss if the input and output are equal? What is the percentage loss if the output is zero (Le. 0(3) = D for all a: E [n', 17]]? (b) Suppose Mr. MacGyver tries several experiments to see which option transmits information with the least loss. In Experiment 1, Mr. MacGyver computes A1 = 0.08. In Experiment 2. Mr. MacGyver computes A2 = 0.14. In which experiment is less information lost? (c) What is the output 01(3) determined by the transistor if the input is 11(x) = 3:2? Do not use approximations but compute the integrals exactly. I _ a: (d) Non.I find the output 03(2) if the input is 12(3) = %. Do not use approximations but compute the integrals exactly. Hint: Use integration by parts twice. Some comments: :1: _ a: o The function at] = % has the name 'hyperbolic sine' and is denoted sinh(:r:). Similarly, one can define the hyperbolic cosine coeh(x). The name 'hyperbolic' is due to the fact that the coordinates (x,y) :- (oosh(t],si.nh(t)) satisfy the equation of a hyperbola 2:2 y: = 1 in a similar way that the coordinates (any) = (008(3), sin(9)) belong to the circle 32 + y"2 = 1. o The expression of 0(3) given above is intimately related to the Fourier transformr which has many applications from solving differential equations to wavelet signal deoomposition. \fExpressions: 14 3000 i. an = en Graph A Graph B ii. an = 2(-1)n+1 2000 0.54 iii. an = (-2)" 1000 iv. an = (-2)" 10 20 30 V. an 10 15 44 Graph C Graph D 2- 0.24 0 10 15 20 0 10 15 -2- 0.4