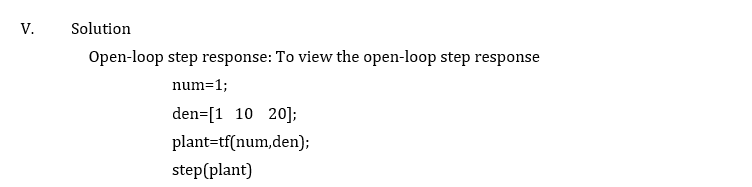
I. II. III. List of Equipment/Software MATLAB LABVIEW Deliverables Summarized learning outcomes LabVIEW programming files Controller design and parameters for each case Procedure: 1. Consider the following unity feedback system: R Controller Plant Plant: A system to be controlled Controller: Provides excitation for the plant: Designed to control the overall system behavior The three-term controller: The transfer function of the PID controller looks like the following Kp ++ KDS KDs+Kps+K1 = S KP Proportional gain KI = Integral gain KD Derivative gain Looking at how the PID controller works in a closed loop system using the schematic shown. The variable (e) represents the tracking error, the difference between the desired input value (R) and the actual output (Y). This error signal (e) will be sent to the PID controller and the controller computes both the derivative and the integral of this error signal. The signal (u) just past the controller is now equal to the proportional gain (KP) times the magnitude of the error plus the integral gain (KI) times the integral of the error plus the derivative gain (KD) times the derivative of the error. u = Kpe(t) + Kf e(t)dt +K de(t) dt This signal (u) will be sent to the plant, and the new output (Y) will be obtained. This new output (Y) will be sent back to the sensor again to find the new error (e). The controller takes this new error signal and computes its derivatives and its internal again. The process goes on and on. IV. Problem Suppose we have a simple mass, spring and damper bx M k The modeling equation of this system is Mx + bx +kx = F Taking the Laplace transform of the modeling equation, we have Msx(s) + bsx(s) + kX(s) = F(s) The transfer function between the displacement X(s) and the input F(s) then becomes Let X(5) F(s) 1 = Ms+bs+k M = 1kg b = 10 N s/m k = 20N/m F(s) = 1 Substitute these values into the above transfer function X(s) F(s) 1 s+10s+20 The goal of this problem is to show how each of Kp, Ki and Ka contributes to obtain Fast rise time Minimum overshoot No steady state error 1. Obtain the unit step response of the system for the different controllers 2. Based on your results, what do you conclude as the best controller for this process? V. Solution Open-loop step response: To view the open-loop step response num=1; den=[1 10 20]; plant-tf(num,den); step(plant) MATLAB command window should give the plot Displacement (m) 0.05 0.04 0.03 0.02 0.01 0 Open-Loop Step 0 0.5 1 1.5 2 Time (sec) The DC gain of the plant transfer function is 1/20, so 0.05 is the final value of the output to a unit step input. This corresponds to the steady-state error of 0.95, quite large. Furthermore, the rise time is about one second, and the settling time is about 1.5 seconds. Design a controller that will reduce the rise time, and the settling time and eliminates the steady-state error. Proportional control: The closed-loop transfer function of the system discussed earlier with a proportional controller is Plant P Controller R u 1 s + 10s + 20 X(s) = F(s) s+10s+(20+Kp) Let the proportional gain (Kp) equal 300 Kp=300; contr=Kp; sys cl=feedback(countr*plant, 1); t=0:0.01:2; step(sys_cl,t) MATLAB command window should give the following plot 1.4 Closed-Loop Step: Kp=300 1.2 Displacement (m) 0.6 0.4 0.2 0 0.5 1 1.5 2 Time (sec) Note: The MATLAB function called feedback was used to obtain a closed-loop transfer function directly from the open-loop transfer function (instead of computing closed-loop transfer function by hand). The above plot shows that the proportional controller reduced both the rise time and the steady state error, increased the overshoot, and decreased the settling time by small amount. Proportional-Derivative control: The closed-loop transfer function of the given system with a PD controller is: PD Controller Kp+Kos u Plant 1 s + 10s + 20 X(s) F(s) = Ks + K s+(10+ K)s + (20+Kp) Let Kp equal 300 as before and let KD equal 10. Kp=300; Kd=10; contr=tf([Kd Kp],1); sys_cl=feedback(contr*plant,1); t=0:0.01:2; step(sys_cl,t) MATLAB command window should give the following plot Displacement (m) Closed-Loop Step: Kp=30 Ki=70 1.4 1.2 1 0.8 0.6 0.4 0.2 0 0 0.5 1.5 2 Time (sec) The proportional gain (Kp) was reduced because the integral controller also reduces the rise time and increases the overshoot as the proportional controller does (double effect). The above response shows that the integral controller eliminated steady-state error. Proportional-Integral-Derivative control: Look at a PID controller. The closed loop transfer function of the given system with a PID controller is Plant PID Controller Kp+K/s+ Kos u 1 s + 10s + 20 X(s) = Ks + Kps + K F(s) s + (10+K)s + (20+K)s + K | After several trial and error, the gains Kp=350, Ki-300 and Kd=50 provided the desired response. To confirm, enter the following commands to an m-file and run it in the command window. The following response should show Kp=350; Ki=300; Kd=50; contr=tf([Kd Kp Ki],[10]); sys_clr=feedback(contr*plant,1); t=0:0.01:2; step(sys_cl,t) Rubric for Checking Criteria (%) 4 Ability to The problem has understand the been clearly and problem fully understood (25%) Ability to 3 The problem was identified and understood 2 The problem was identified but not understood 1 The problem was not understood formulate engineering solutions to the given problem (25%) Ability to apply the best solution to the problem (25%) Identify the effect of the solutions to the real world (25%) Presents a detailed step by step solution to the problem Presents a general approach to solve the problem The correct solution to the problem has been clearly presented Can identify and explain several effects of solution to the real world The solution to the problem has not been fully elaborated Can identify and explain one effect of the solution to the real world Presents an idea of the solution to the problem Unable to make appropriate solution to the problem The full solution to the problem has not been achieved Can identify only one effect of the solution to the real world Not able to solve the problem Cannot identify the effect of the solution to the real world