Question
I need help with this problem please The harmonic series is defined as the sum: The series diverges, but slowly, like ln(n). A good approximation
I need help with this problem please
The harmonic series is defined as the sum:
The series diverges, but slowly, like ln(n). A good approximation to is given by the formula:
where = 0.57721 is so-called Euler-Mascheroni constant. ( - greek letter, gamma)
An improved approximation to is given by:
(1) create a vector n, where n start at 1, end as 20 with increment of 1.
(2) Calculate the approximation of using , use variable name f_n.
(3) Calculate the approximation of using , use variable name g_n.
(4) Convert f_n and g_n to column vectors, and put them in a matrix named table_approx. In the matrix, the first column is f_n, second of the table is g_n.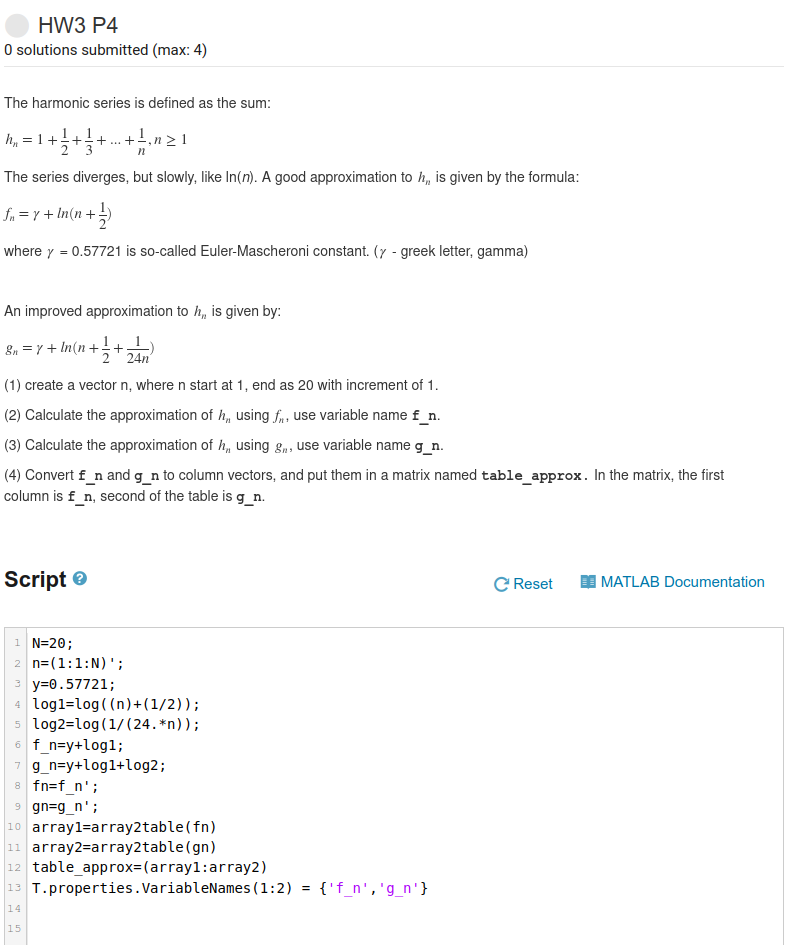
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


