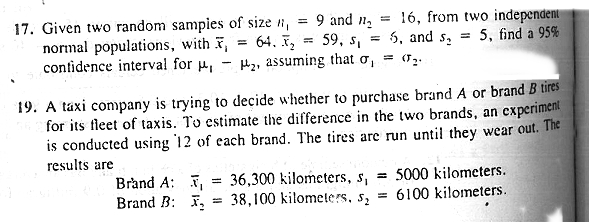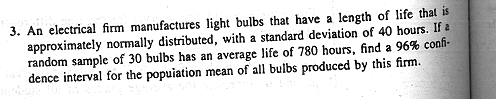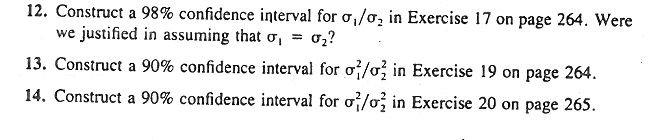I need the following answers solutions from the attached exercise which is Chapter # 9
Estimation of Parameters. Books is Introduction to Statistics (3rd Edition) by Ronald E.Walpole_ for reference.
Questions:
Page #262-266 Question # 3, 4, 13, 15, 16, 17, 19, 20, 21, 23
Page #283 Question # 12, 13, 14
- All questions solve only by t distribution or F distribution
- In case you will not find the value of t-distribution or f-distribution in the table given in the book, then use Excel
- In all questions, develop 95% confidence interval.
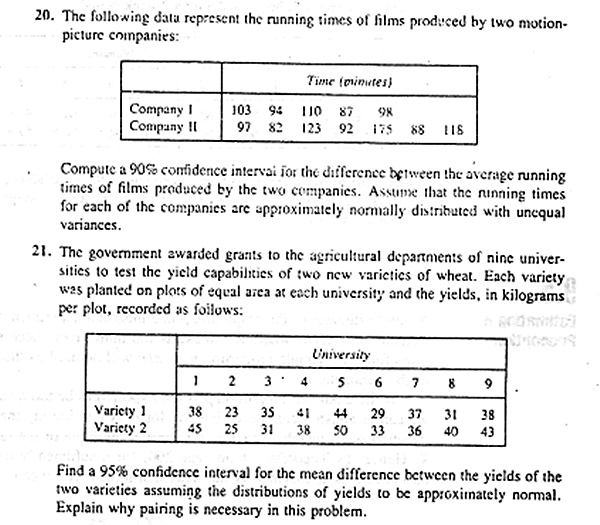
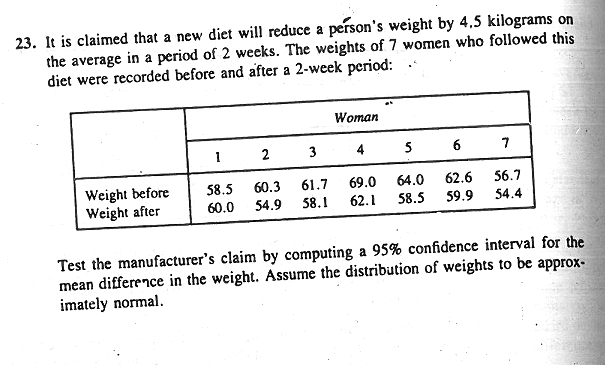
13. A random sample of 12 female students in a certain dormitory showed an average weekly expenditure of $8.00 for snack foods, with a standard deviation of $1.75. Construct a 90% confidence interval for the average amount spent each week on snack foods by female students living in this dormitory . assuming the expenditures to be approximately normally distributed. 15. Two kinds of thread are being compared for strength. Fifty pieces of each type of thread are tested under similar conditions. Brand A had an average tensile strength of 78.3 kilograms with a standard deviation of 5.6 kilograms, while brand B had an average tensile strength of 87.2 kilograms with a standard devia- tion of 6.3 kilograms. Construct a 95 confidence interval for the difference of the population means. 16. A study was made to estimais the chference in salaries of college professors in the private and state colleges of Virginia. A random sample of 100 professors in private colleges showed an average 9-month salary of $25,000 with a standard deviation of $1200. A random sample of 200 professors in state colleges showed an average salary of $26.000 with a standard deviation of $1400. Find a 98% confidence interval for the difference between the average salaries of professors teaching in state and private colleges of Virginia.17. Given two random samples of size /, = 9 and n, = 16, from two independent normal populations, with * = 64. x, = 59, s, = 6, and s, = 5, find a 95% confidence interval for p - p2, assuming that 0, = (2. 19. A taxi company is trying to decide whether to purchase brand A or brand B tires for its fleet of taxis. To estimate the difference in the two brands, an experiment is conducted using 12 of each brand. The tires are run until they wear out. The results are Brand A: = 36,300 kilometers, s, = 5000 kilometers. Brand B: = 38,100 kilometers. s, = 6100 kilometers.20. The following data represent the running times of films produced by two motion- picture companies: Time (minutes) Company I 103 94 110 87 Company II 97 82 123 92 175 $8 116 Compute a 90% confidence interval for the difference between the average running times of films produced by the two companies. Assume that the ninning times for each of the companies are approximately normally distributed with unequal variances. 21. The government awarded grants to the agricultural departments of nine univer- sities to test the yield capabilities of two new varieties of wheat. Each variety was planted on plots of equal area at each university and the yields, in kilograms per plot, recorded as follows: University 1 2 34 5 6 7 9 Variety 1 38 23 35 41 44. 29 37 31 38 Variety 2 45 25 31 38 50 33 36 40 43 Find a 95% confidence interval for the mean difference between the yields of the two varieties assuming the distributions of yields to be approximately normal. Explain why pairing is necessary in this problem.23. It is claimed that a new diet will reduce a person's weight by 4.5 kilograms on the average in a period of 2 weeks. The weights of 7 women who followed this diet were recorded before and after a 2-week period: Woman 2 3 4 5 6 7 Weight before 58.5 60.3 61.7 69.0 64.0 62.6 56.7 Weight after 60.0 54.9 58.1 62.1 58.5 59.9 54.4 Test the manufacturer's claim by computing a 95% confidence interval for the mean difference in the weight. Assume the distribution of weights to be approx- imately normal.3. An electrical firm manufactures light bulbs that have a length of life that is approximately normally distributed, with a standard deviation of 40 hours. If a random sample of 30 bulbs has an average life of 780 hours, find a 96% confi- dence interval for the population mean of all bulbs produced by this firm.4. A soft-drink machine is regulated so that the amount of drink dispensed is ap- . proximately normally distributed with a standard deviation equal to 1.5 deciliters. Find a 95% confidence interval for the mean of all drinks dispensed by this machine if a random sample of 36 drinks had an average content of 22.5 deciliters.12. Construct a 98% confidence interval for of /o, in Exercise 17 on page 264. Were we justified in assuming that o, = 02? 13. Construct a 90% confidence interval for of/o; in Exercise 19 on page 264. 14. Construct a 90% confidence interval for of/o; in Exercise 20 on page 265