
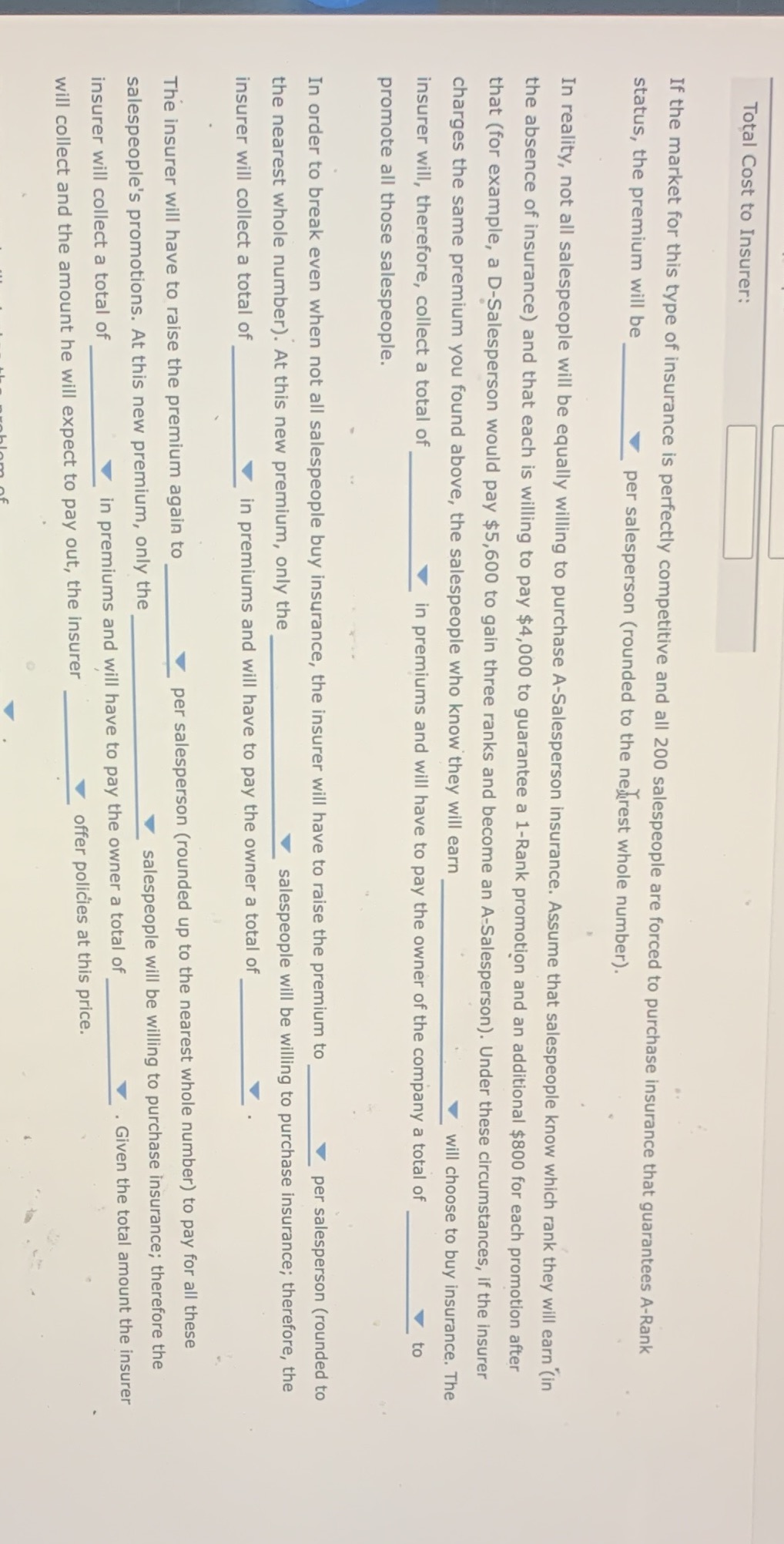
If the market for this type of insurance is perfectly competitive and all 200 salespeople are forced to purchase insurance that guarantees A-Rank status, the premium will be $3510/1500/4333/3900 per salesperson (rounded to the nearest whole number). In reality, not all salespeople will be equally willing to purchase A-Salesperson insurance. Assume that salespeople know which rank they will earn (in the absence of insurance) and that each is willing to pay $4,000 to guarantee a 1-Rank promotion and an additional $800 for each promotion after that (for example, a D-Salesperson would pay $5,600 to gain three ranks and become an A-Salesperson). Under these circumstances, if the insurer charges the same premium you found above, the salespeople who know they will earn A- and B- rank/ B and C rank/ A,B,C and D rank/ B, C and D rank will choose to buy insurance. The insurer will, therefore, collect a total of $270000/ 780000/ 702000/631800 in premiums and will have to pay the owner of the company a total of $14400/702000/780000/631800___to promote all those salespeople. In order to break even when not all salespeople buy insurance, the insurer will have to raise the premium to per salesperson (rounded to the nearest whole number). At this new premium, only the C- and D rank/ B,D and C rank/ D rank salespeople will be willing to purchase insurance; therefore, the insurer will collect a total of $680000/779940/619619/563290 in premiums and will have to pay the owner a total of $779940/ 680000/ 563290/619619. The insurer will have to raise the premium again $5231/7041/8500 to per salesperson (rounded up to the nearest whole number) to pay for all these salespeople's promotions. At this new premium, only the D rank/ C and D rank/ B C and D rank salespeople will be willing to purchase insurance; therefore the insurer will collect a total of $381304/480000/563290/418480 in premiums and will have to pay the owner a total of $418480/563290/381304/480000. Given the total amount the insurer will collect and the amount he will expect to pay out, the insurer will/will not offer policies at this price. The above example illustrates the problem of moral hazard/ adverse selection.
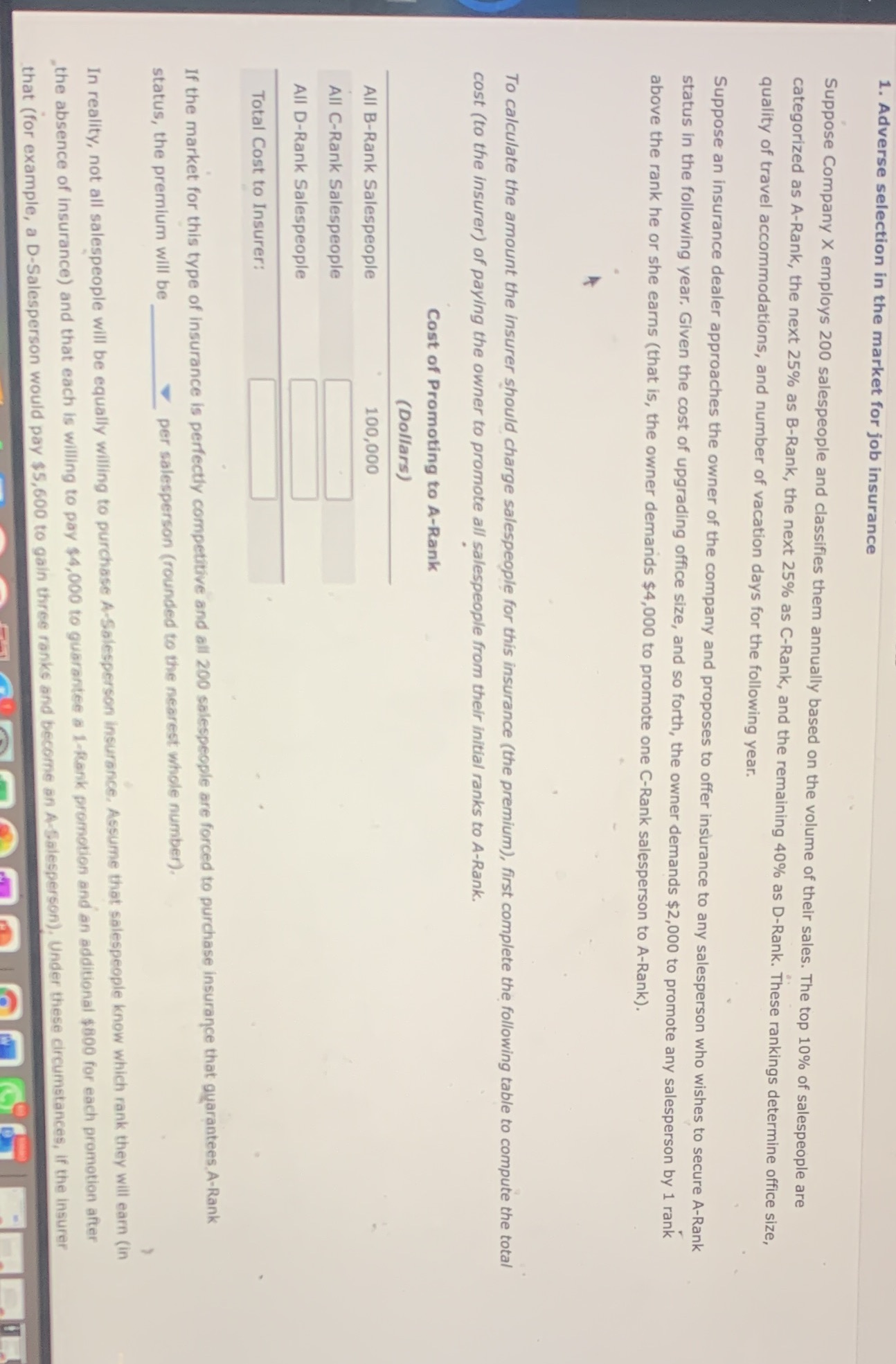
1. Adverse selection in the market for job insurance Suppose Company X employs 200 salespeople and classifies them annually based on the volume of their sales. The top 10% of salespeople are categorized as A-Rank, the next 25% as B-Rank, the next 25% as C-Rank, and the remaining 40% as D-Rank. These rankings determine office size, quality of travel accommodations, and number of vacation days for the following year. Suppose an insurance dealer approaches the owner of the company and proposes to offer insurance to any salesperson who wishes to secure A-Rank status in the following year. Given the cost of upgrading office size, and so forth, the owner demands $2,000 to promote any salesperson by 1 rank above the rank he or she earns (that is, the owner demands $4,000 to promote one C-Rank salesperson to A-Rank). To calculate the amount the insurer should charge salespeople for this insurance (the premium), first complete the following table to compute the total cost (to the insurer) of paying the owner to promote all salespeople from their initial ranks to A-Rank. Cost of Promoting to A-Rank (Dollars) All B-Rank Salespeople 100,000 All C-Rank Salespeople All D-Rank Salespeople Total Cost to Insurer: If the market for this type of insurance is perfectly competitive and all 200 salespeople are forced to purchase insurance that guarantees. A-Rank status, the premium will be per salesperson (rounded to the nearest whole number). In reality, not all salespeople will be equally willing to purchase A-Salesperson insurance, Assume that salespeople know which rank they will earn (in the absence of insurance) and that each is willing to pay $4,000 to guarantee a 1-Rank promotion and an additional $800 for each promotion after that (for example, a D-Salesperson would pay $5,600 to gain three ranks and become an A-Salesperson), Under these circumstances, if the insurer1. Adverse selection in the market for job insurance Suppose Company X employs 200 salespeople and classifies them annually based on the volume of their sales. The top 10% of salespeople are categorized as A-Rank, the next 25% as B-Rank, the next 25% as C-Rank, and the remaining 40% as D-Rank. These rankings determine office size, quality of travel accommodations, and number of vacation days for the following year. Suppose an insurance dealer approaches the owner of the company and proposes to offer insurance to any salesperson who wishes to secure A-Rank status in the following year. Given the cost of upgrading office size, and so forth, the owner demands $2,000 to promote any salesperson by 1 rank above the rank he or she earns (that is, the owner demands $4,000 to promote one C-Rank salesperson to A-Rank). To calculate the amount the insurer should charge salespeople for this insurance (the premium), first complete the following table to compute the total cost (to the insurer) of paying the owner to promote all salespeople from their initial ranks to A-Rank. Cost of Promoting to A-Rank (Dollars) All B-Rank Salespeople 100,000 All C-Rank Salespeople All D-Rank Salespeople Total Cost to Insurer: If the market for this type of insurance is perfectly competitive and all 200 salespeople are forced to purchase insurance that guarantees A-Rank status, the premium will be per salesperson (rounded to the nearest whole number).Total Cost to Insurer: If the market for this type of insurance is perfectly competitive and all 200 salespeople are forced to purchase insurance that guarantees A-Rank status, the premium will be per salesperson (rounded to the nearest whole number). In reality, not all salespeople will be equally willing to purchase A-Salesperson insurance. Assume that salespeople know which rank they will earn (in the absence of insurance) and that each is willing to pay $4,000 to guarantee a 1-Rank promotion and an additional $800 for each promotion after that (for example, a D-Salesperson would pay $5,600 to gain three ranks and become an A-Salesperson). Under these circumstances, if the insurer charges the same premium you found above, the salespeople who know they will earn will choose to buy insurance. The insurer will, therefore, collect a total of in premiums and will have to pay the owner of the company a total of promote all those salespeople. In order to break even when not all salespeople buy insurance, the insurer will have to raise the premium to per salesperson (rounded to the nearest whole number). At this new premium, only the salespeople will be willing to purchase insurance; therefore, the insurer will collect a total of in premiums and will have to pay the owner a total of The insurer will have to raise the premium again to per salesperson (rounded up to the nearest whole number) to pay for all these salespeople's promotions. At this new premium, only the salespeople will be willing to purchase insurance; therefore the insurer will collect a total of in premiums and will have to pay the owner a total of . Given the total amount the insurer will collect and the amount he will expect to pay out, the insurer offer policies at this price












