import java.lang.Math.*;

class expressionTreeNode { private String value; private expressionTreeNode leftChild, rightChild, parent; expressionTreeNode() { value = null; leftChild = rightChild = parent = null; } // Constructor /* Arguments: String s: Value to be stored in the node expressionTreeNode l, r, p: the left child, right child, and parent of the node to created Returns: the newly created expressionTreeNode */ expressionTreeNode(String s, expressionTreeNode l, expressionTreeNode r, expressionTreeNode p) { value = s; leftChild = l; rightChild = r; parent = p; } /* Basic access methods */ String getValue() { return value; }

expressionTreeNode getLeftChild() { return leftChild; }

expressionTreeNode getRightChild() { return rightChild; }

expressionTreeNode getParent() { return parent; }

/* Basic setting methods */ void setValue(String o) { value = o; } // sets the left child of this node to n void setLeftChild(expressionTreeNode n) { leftChild = n; n.parent = this; } // sets the right child of this node to n void setRightChild(expressionTreeNode n) { rightChild = n; n.parent=this; }

// Returns the root of the tree describing the expression s // Watch out: it makes no validity checks whatsoever! expressionTreeNode(String s) { // check if s contains parentheses. If it doesn't, then it's a leaf if (s.indexOf("(")==-1) setValue(s); else { // it's not a leaf

/* break the string into three parts: the operator, the left operand, and the right operand. ***/ setValue( s.substring( 0 , s.indexOf( "(" ) ) ); // delimit the left operand 2008 int left = s.indexOf("(")+1; int i = left; int parCount = 0; // find the comma separating the two operands while (parCount>=0 && !(s.charAt(i)==',' && parCount==0)) { if ( s.charAt(i) == '(' ) parCount++; if ( s.charAt(i) == ')' ) parCount--; i++; } int mid=i; if (parCount

// recursively build the left subtree setLeftChild(new expressionTreeNode(s.substring(left,mid))); if (parCount==0) { // it is a binary operator // find the end of the second operand.F13 while ( ! (s.charAt(i) == ')' && parCount == 0 ) ) { if ( s.charAt(i) == '(' ) parCount++; if ( s.charAt(i) == ')' ) parCount--; i++; } int right=i; setRightChild( new expressionTreeNode( s.substring( mid + 1, right))); } } }

// Returns a copy of the subtree rooted at this node... 2014 expressionTreeNode deepCopy() { expressionTreeNode n = new expressionTreeNode(); n.setValue( getValue() ); if ( getLeftChild()!=null ) n.setLeftChild( getLeftChild().deepCopy() ); if ( getRightChild()!=null ) n.setRightChild( getRightChild().deepCopy() ); return n; } // Returns a String describing the subtree rooted at a certain node. public String toString() { String ret = value; if ( getLeftChild() == null ) return ret; else ret = ret + "(" + getLeftChild().toString(); if ( getRightChild() == null ) return ret + ")"; else ret = ret + "," + getRightChild().toString(); ret = ret + ")"; return ret; }

// Returns the value of the expression rooted at a given node // when x has a certain value double evaluate(double x) { // WRITE YOUR CODE HERE

// AND CHANGE THIS RETURN STATEMENT return 0; }

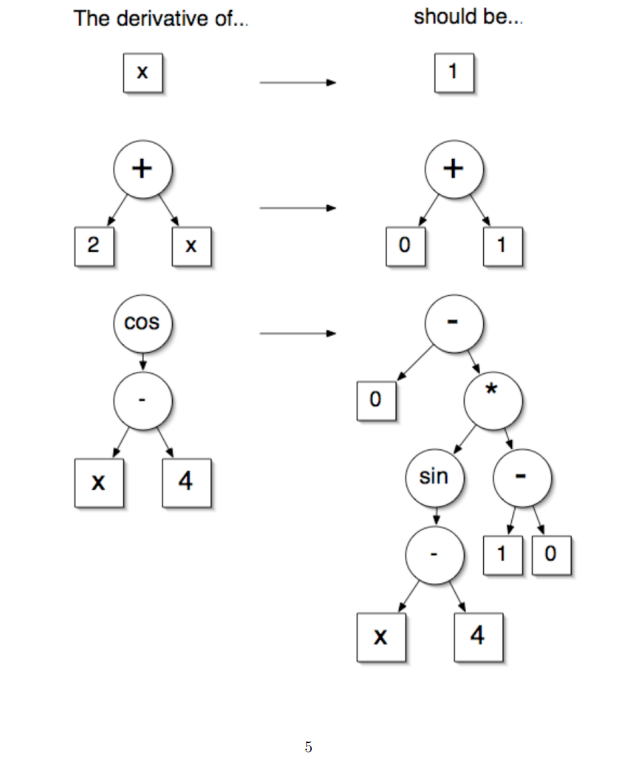
/* returns the root of a new expression tree representing the derivative of the original expression */ expressionTreeNode differentiate() { // WRITE YOUR CODE HERE

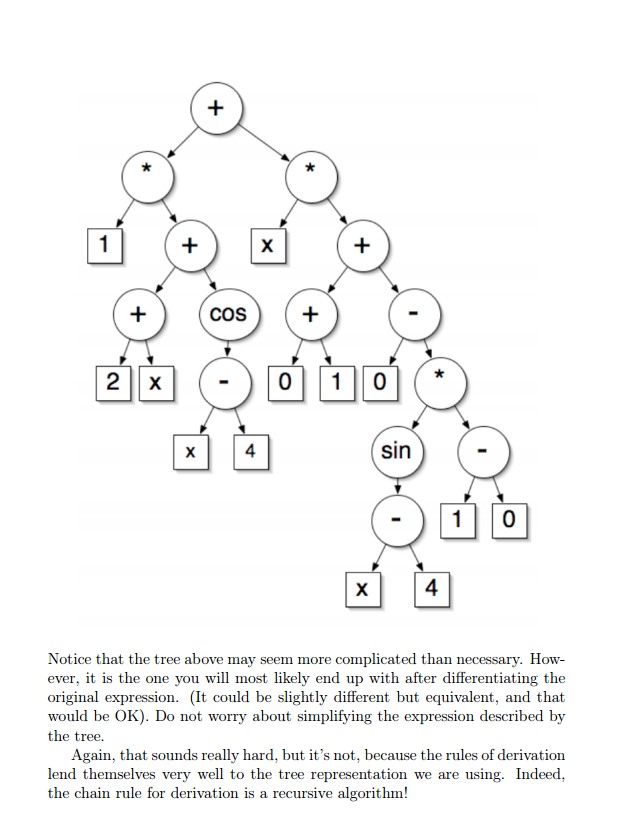
// AND CHANGE THIS RETURN STATEMENT return null; } public static void main(String args[]) { expressionTreeNode e = new expressionTreeNode("mult(add(2,x),cos(x))"); System.out.println(e); System.out.println(e.evaluate(1)); System.out.println(e.differentiate()); } }

3. More on Expression Trees, 25 pts We have seen in class how such expressions can be represented using a binary tree where internal nodes correspond to operator x, sin, cos, exp) and leaves are the operands. For example, the expression ax ((2 r) cos(a -4)) can be represented as: COS The code (see provides you with a binary tree data structure for storing expressions. It contains a constructor that takes as input a string describing an expression and returns the root of the binary tree storing that expression. The string describing the expression is in the following format The only operators considered are add, mult, minus, sin, cos, and exp Each operator is followed by its operand(s) in parentheses If there are two operands, they are separated by a comma. We only consider expressions with a single variable called x. Thus the mathematical expression arx (2+z)+cos(r-4)) should be written mult(x, add(add(2, x) cos (minus(x, 4))))