Ive had some trouble in understanding and building for this past assignment:

Yeah! Since this is the lastest quest of this level, it is also gonna be the funnest quest.

You get to implement a simple Graph data structure with a WHOLE LOT OF freedom around how you do it.

All you have to do in this quest is to make various shapes. I don't care how you make them as long as you make them correctly.

Pick and choose. Each shape is worth a certain number of rewards. Generally, the simpler ones are also cheaper and easier to get.

But before you get to it, here's the representation I'll be looking for:

class Graph {

protected:

struct Edge {

int _dst;

std::string _tag;

Edge(int dst = -1, std::string tag = "") : _dst(dst), _tag(tag) {}

};

std::vector<:vector> > _nodes;

// Suggested private helpers. Not tested.

void add_edge(int src, int dst, std::string tag);

std::string to_string() const;

public:

void make_silly_snake();

void make_mr_sticky();

void make_driftin_dragonfly();

void make_slinky_star();

void make_kathy_da_grate();

void make_dodos_in_space();

void make_purty_pitcher();

friend class Tests; // Don't remove this line.

};

We're keeping everything as simple as possible so you can focus on your visual art in this quest. Our Graph nodes only have numbers, not names. Edges from one node to another may have optional string tags you can stick on them.

This lets us model the graph as a collection of nodes which each contain a collection of edges. This is it:

std::vector<:vector> > g;

where the entire graph is simply the collection of nodes, called g above. In this case, we're using

vectors for collections.

Important: The graph is NOT a 2D matrix. It is a vector of nodes, where each node contains a vector of edges. Nodes that don't have edges leaving them will be represented by the cells that hold empty vectors. Put another way, the edge from node A to node B can be found in the vector located at g[A]. But that edge is NOT g[A][B]. Instead you must scan this inner vector to find the edge with the destination of interest.

If you think about it, the Edge object is already an added level of complexity that serves only a cosmetic purpose. We could have made the inner vector a vector of ints, where the ints stand for the destination nodes, and thereby kept things much simpler (We'd still get our shapes).

The reason I have it is to give me a way to stick a label on each edge. I thought it'd be cool. I'll revisit this decision later. For now, it's needed to pass this quest.

Note the golden comment in the starter code. The suggested helper methods are NOT tested. The only methods you need to implement are the public ones, described below in the miniquests. Feel free to implement or not implement the suggested helpers, or implement as many more as you want.

The only thing the miniquests will be looking for is whether your Graph object looks like what it's looking for (in hyper-space, of course. No serialization required).

See I told you it's gonna be fun.

Your first optional miniquest - The Silly Snake Implement:

void Graph::make_silly_snake();

When invoked, it should clear itself and be reborn as a silly snake. See Figure 1.

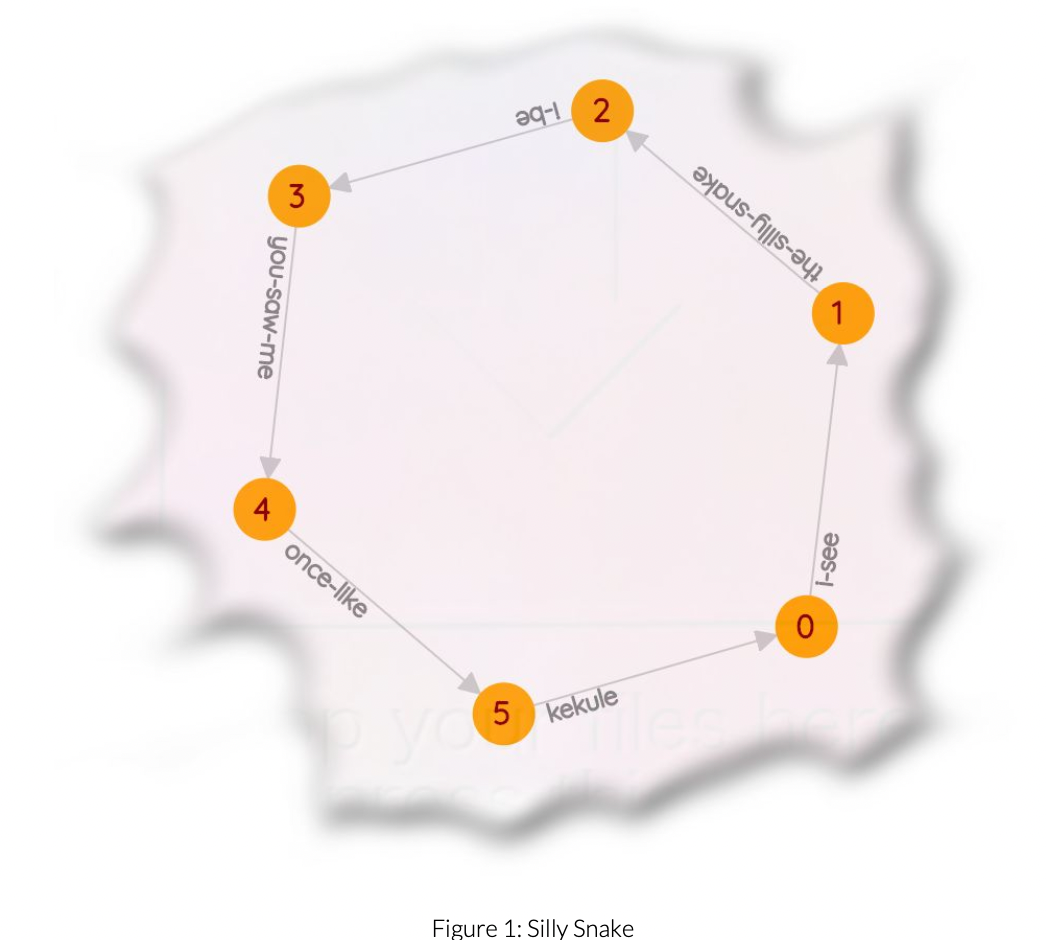
Make sure to get the labels correct.

Your second optional miniquest - Mr Sticky

Implement:

void Graph::make_mr_sticky();

When invoked, it should clear itself and be reborn as a mr sticky. See Figure 2.

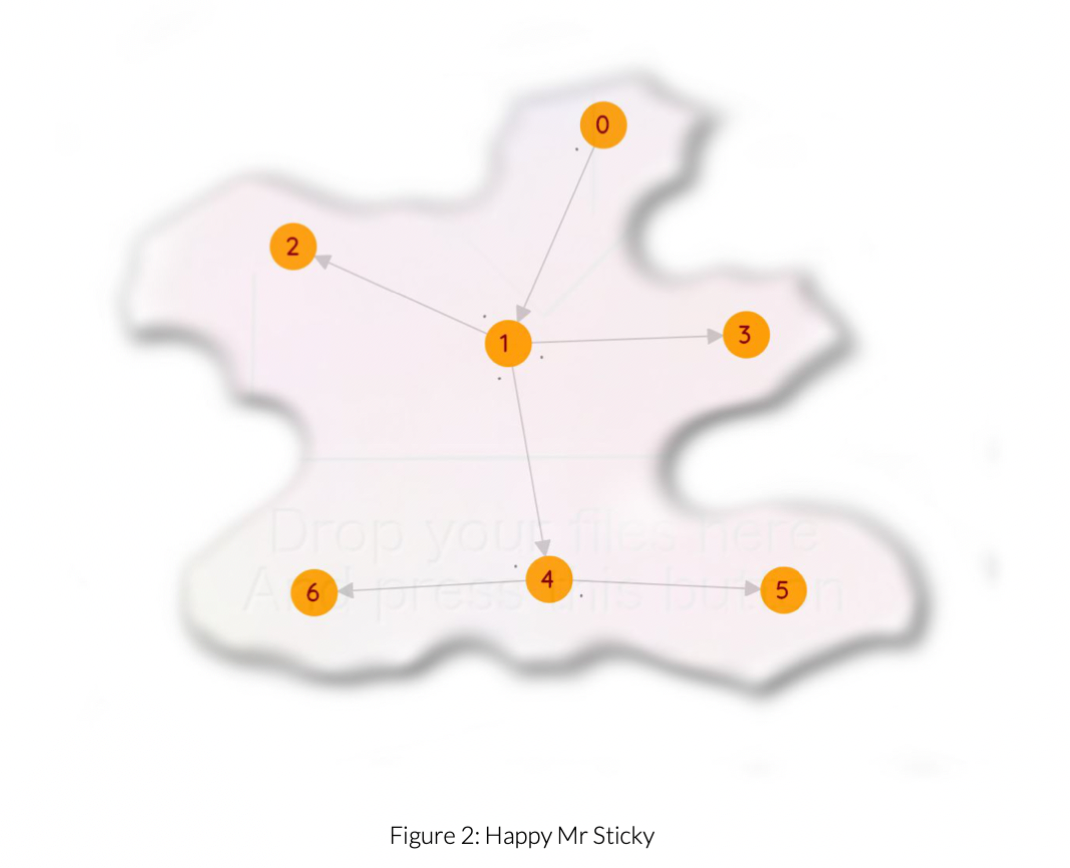
What are the edge labels here? Hmmm... I can't quite tell. Is that a period? Or a hyphen? Oh well, there's only 64 possibilities (or is it 729?)

Your third optional miniquest - The Driftin Dragonfly

Implement:

void Graph::make_driftin_dragonfly();

When invoked, it should clear itself and be reborn as a driftin dragonfly. See Figure 3.

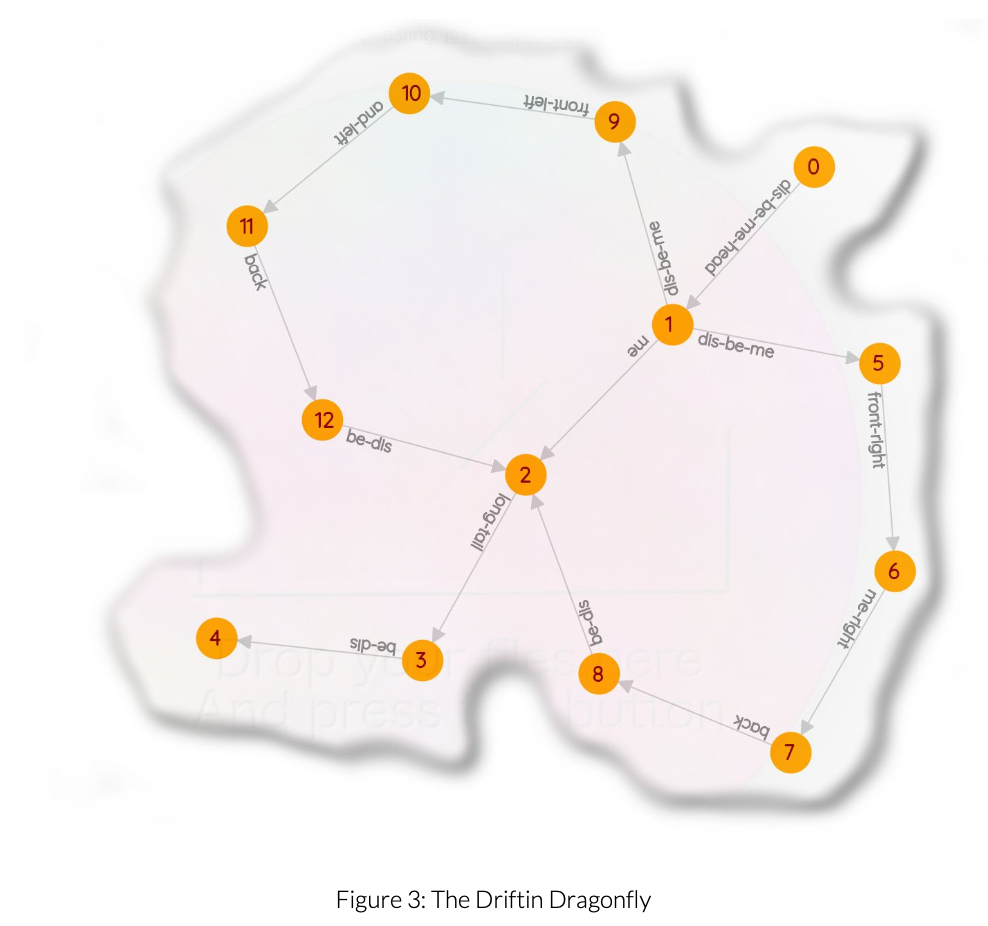
Again, make sure you get the edge labels right, or your dragon don't fly.

Your fourth optional miniquest - The Slinky Star

Implement:

void Graph::make_slinky_star();

When invoked, it should clear itself and be reborn as a slinky star. See Figure 4.

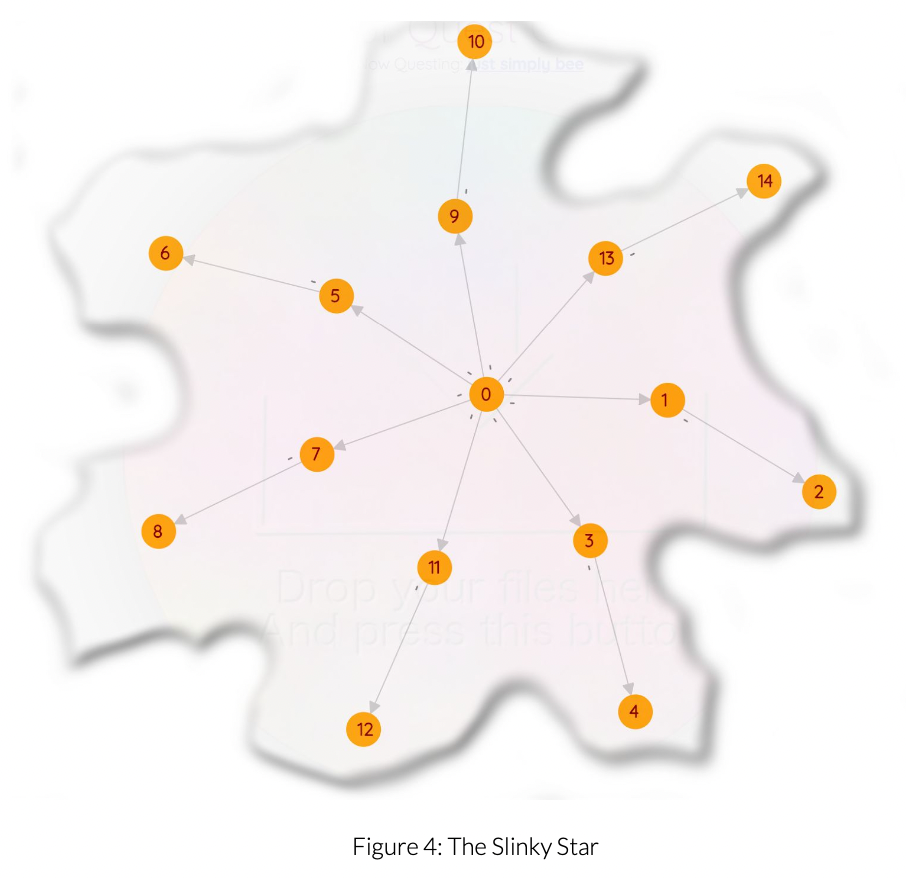
A star you are. A star you be,

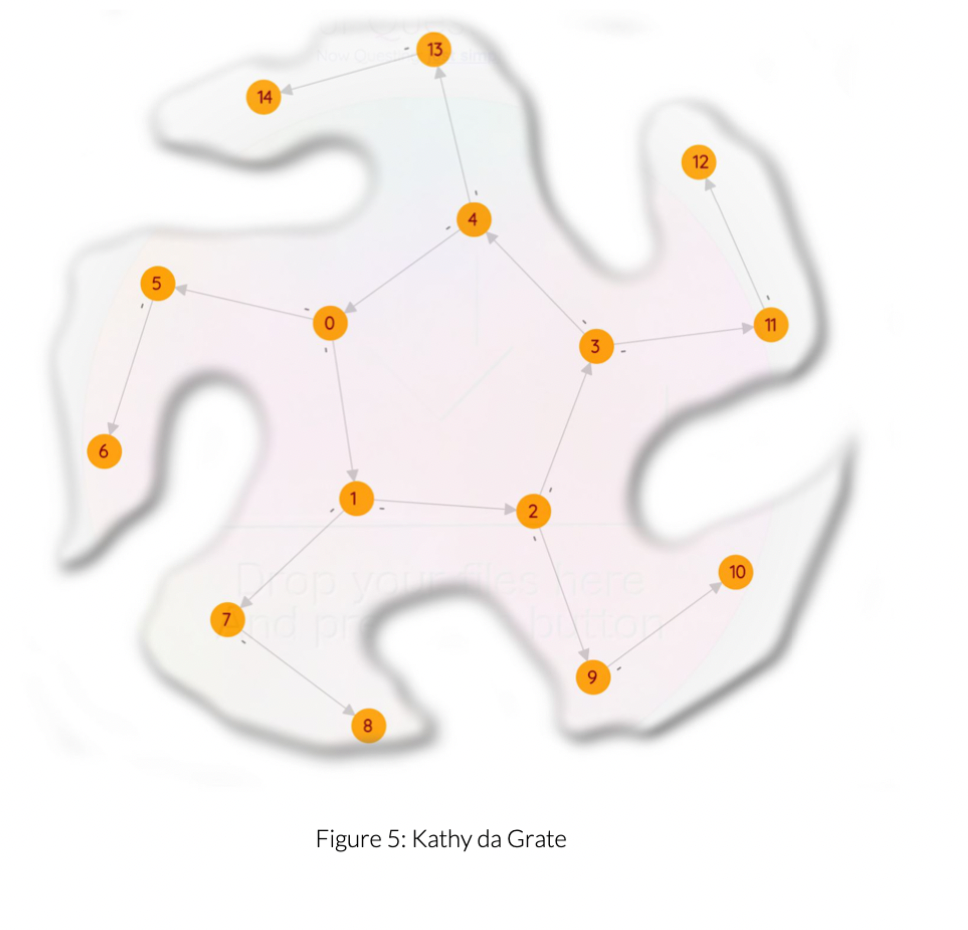
Your fifth optional miniquest - Kathy da grate

Implement:

void Graph::make_kathy_da_grate();

When invoked, it should clear itself and be reborn as Kathy da Grate. See Figure 5.

Your sixth optional miniquest - Dodos in space

Implement:

void Graph::make_dodos_in_space();

When invoked, it should clear itself and be reborn as 25 dodos in space.

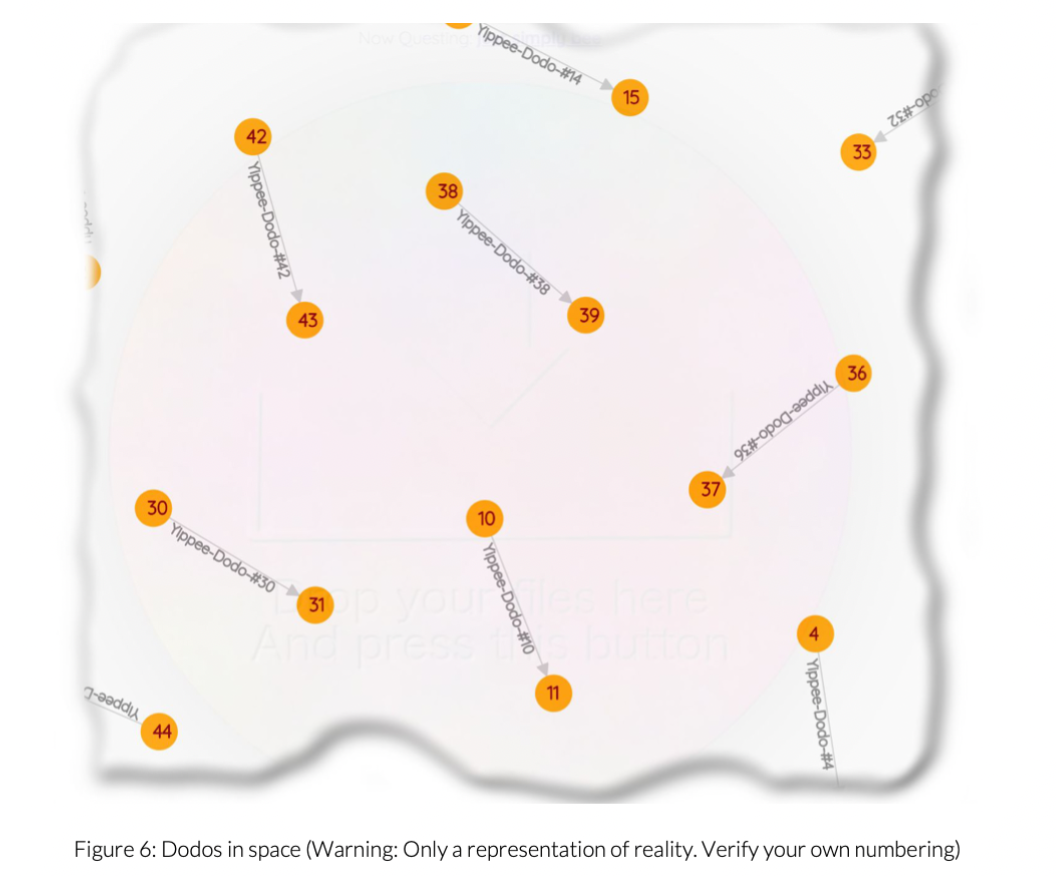
Each dodo is an even numbered node which points to the next odd numbered node via an edge

that is tagged 'Yippee-Dodo-#' post-fixed with the dodo's node number. There should be 25 free dodos in your graph. See Figure 6. The first dodo is numbered #0 and the rest are sequentially numbered after that.

Your seventh optional miniquest - Purty Pitcher

Implement

void Graph::make_purty_pitcher();

It can make any graph you want. If it's purty nuff, upvotes on our subreddit earn extra credit rewards.

Here's mine. Yours don't have to be like dis.

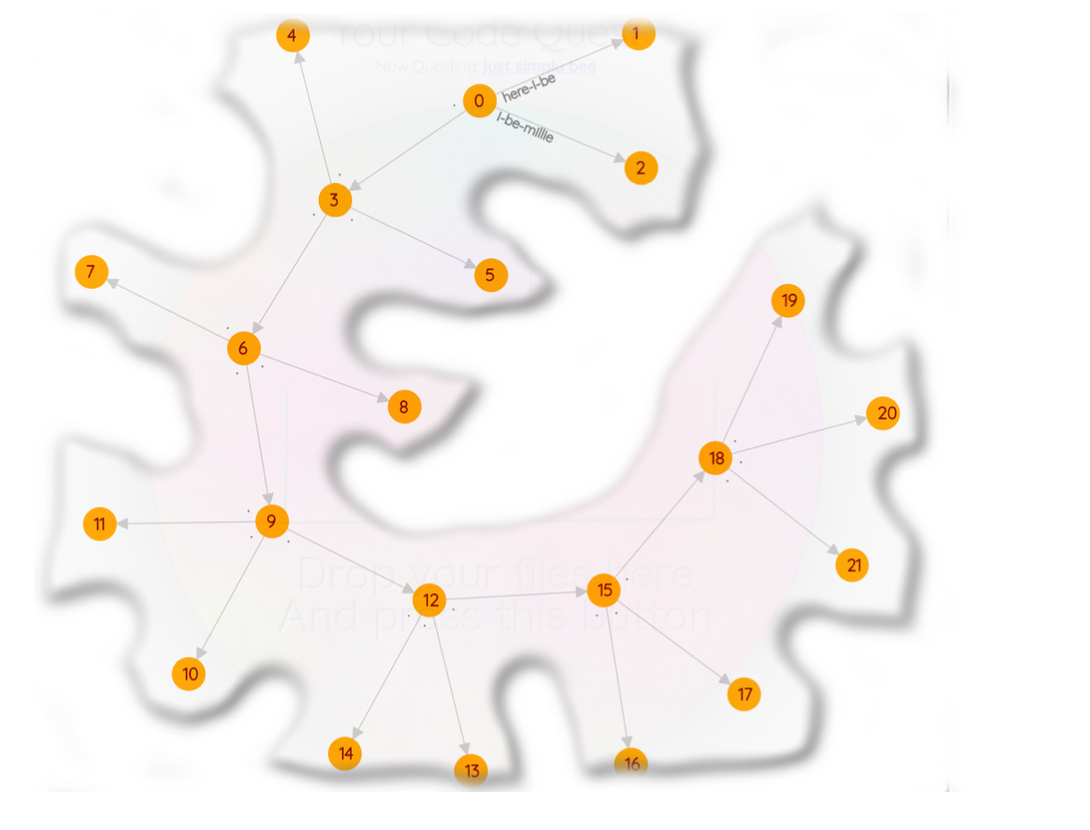
Knock yerselves out.

Figure 1: Silly Snake Figure 2: Happy Mr Sticky Figure 3: The Driftin Dragonfly Figure 4: The Slinky Star Figure 6: Dodos in space (Warning: Only a representation of reality. Verify your own numbering)