JUST DO THE QUESTIONS WITH THE RED X NEXT TO THEM. the other are correct.
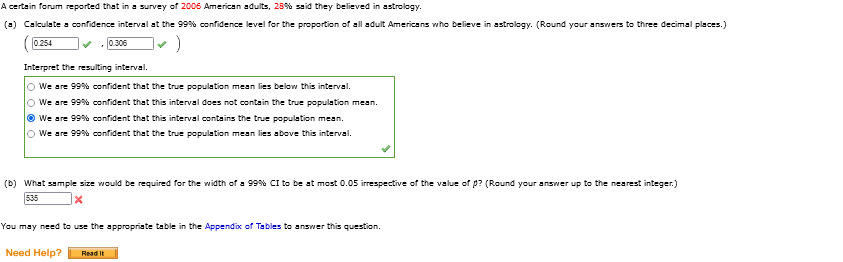
An article contained the 'Following observations on degree of polymerization For paper specimens for which viscosity times concentration Fell in a certain middle range: 413" 420 4-22 4-23 425 428 431. 4-35 433' 433 4-4-5 4-4? 4-45! 452 4-55 4-51. 454 {a} Construct a boxplot of the data. *. O 42!! 430 4-40 450 4-60 0 4-20 4311} 444] 45!) n_n_l_n_n_n_n_I_-_-_-_n_|_n_._._._l_n_n_n_n_l_n_n_ n_n_l_n_n_n_n_I_-_-_-_n_l_n_n_._n_l_n_._n_n_l_n_n_ O 42D 43C! 440 450! 4-61] O 426 43C! 440 45D 4-60 Comment on any interesting features. {Select all that apply.) l:| The data is strongly skewed. I:| The data appears to be centered near 428. I:| There is one outlier. u The data appears to be centered near 4-38. There are no outliers. There is little or no skew. (b) Is it plausible that the given sample observations were selected From a normal distribution? '3' Yes Ohio 1' (c) Calculate a two-sided 95% confidence interval For true average degree oF polymerization. [Round your answers to two decimal places.) (430.30 x ,44523 x ) Does the interval suggest that 4-4-3 is a plausible value For true average degree of polymerization? 'l'es Ohio if Does the interval suggest that 453 is a plausible value? OYes No W You may need to use the appropriate table in the Appendix of Tabla to answer this question. Need Help? Assume that the helium porosity (in percentage) of coal samples taken from any particular seam is normally distributed with true standard deviation 0.70. (=) Compute = 95% CI for the true average porosity of a certain seam if the average porosity for 25 specimens from the seam was 4.85. (Round your answers to two decimal places.) 4.24 X . 5.46 x ) (b) Compute = 98%% CI for true average porosity of another seam based on 15 specimens with a sample average porosity of 4.56. (Round your answers to two decimal places.) 4.14 4.93 (c) How large a sample size is necessary if the width of the 95% interval is to be 0.32? (Round your answer up to the nearest whole number.) 74 specimens (d) What sample size is necessary to estimate true average porosity to within 0.23 with 99% confidence? (Round your answer up to the nearest whole number.) 246 * specimens You may need to use the appropriate table in the Appendix of Tables to answer this question. Need Help? Roud It Which ItA certain forum reported that in a survey of 2006 American adults, 28% said they believed in astrology. (=) Calculate a confidence interval at the 98%% confidence level for the proportion of all adult Americans who believe in astrology. (Round your answers to three decimal places.) 0.254 . 0.306 Interpret the resulting interval. O We are 98%% confident that the true population mean lies below this interval. O We are 98%% confident that this interval does not contain the true population mean. 0 We are 98%% confident that this interval contains the true population mean. O We are 99%% confident that the true population mean lies above this interval. (b) What sample size would be required for the width of a 98% CI to be at most 0.05 irrespective of the value of ? ( Round your answer up to the nearest integer.) 535 x You may need to use the appropriate table in the Appendix of Tables to answer this question. Need Help? Read ItTV advertising agencies face increasing challenges in reaching audience members because viewing TV programs vis digital streaming is gaining in popularity. A poll reported that 54%% of 2349 American adults surveyed said they have watched digitally streamed TV programming on some type of device. (=) Calculate and interpret a confidence interval at the 98%% confidence level for the proportion of all adult Americans who watched streamed programming up to that point in time. (Round your answers to three decimal places.) 0.514 0.566 Interpret the resulting interval. O We are 98%% confident that this interval does not contain the true population proportion. 3 We are 98%% confident that this interval contains the true population proportion. O We are 98%% confident that the true population proportion lies above this interval. O We are 99%% confident that the true population proportion lies below this interval. (b) What sample size would be required for the width of = 98%% CI to be at most 0.04 irrespective of the value of ? ( Round your answer up to the nearest integer.) 1030 X You may need to use the appropriate table in the Appendix of Tables to answer this question. Need Help? Road IE