Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Let A be a DFA that accepts all strings over the alphabet {1,0} that contain either the substring 10 or 01 (non-exclusive, i.e. both can
Let A be a DFA that accepts all strings over the alphabet {1,0} that contain either the substring 10 or 01 (non-exclusive, i.e. both can be contained as substrings)., and consider the string w = 001011. Confirm that w L(A) , by showing that (p0, w) F where q0 is the start state of A and F is its finish states. You have to show this formally using the inductive definition of . (Start with (q0, 0) and then (q0, 00) and then (q0, 001) and so on...)
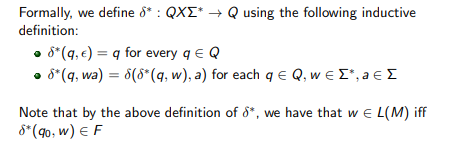
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


