Question: Let f(x) = + 1 Za[r] and let R = Za[r]/I, where I = (f(x)). (a) Show that R is a field with 9

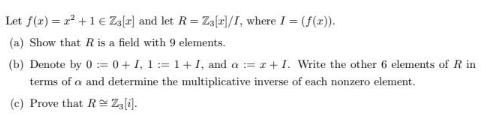
Let f(x) = + 1 Za[r] and let R = Za[r]/I, where

Let f(x) = + 1 Za[r] and let R = Za[r]/I, where I = (f(x)). (a) Show that R is a field with 9 elements. (b) Denote by 0 = 0+1, 1 = 1 + 1, and a :=z+I. Write the other 6 elements of R in terms of a and determine the multiplicative inverse of each nonzero element. (e) Prove that RZ[i].

Step by Step Solution

★★★★★

3.54 Rating (151 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a We must confirm two features in order to demonstrate that R is a field with nine elements Each non... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let z = ((x, y), where x = r cos ( and y = r sin (. Show that dr

Let f : R x R R be differentiable. For each x R defined gx: R R By gx (y) = f(x,y). Suppose that for each x there is a unique y with gx1(y) =0; let c(x) be this y.

Let f : R R. Prove that f is continuous on R if and only if f-1 (I) is open in R for every open interval I.

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

HW 12, MAT 312/AMS 351: SPRING 2017 Problem 1. (1) Set H = {4a + 6b | a, b Z} Z. Show that H is a subgroup of Z. (2) Is H cyclic? Problem 2. Write down all the cyclic subgroups of the following...

Give Correct ANSWERS Human-Computer Interaction (a) If you had been one of the original inventors of the WIMP interface, and engineers on the technical team had been sceptical about the advantages...

Top Purse Company applies the periodic inventory system using the specific identification method. The company had the following transactions related to its best selling purse. Date Transaction Units...

Pharmaceutical Benefits Managers (PBMs) are intermediaries between upstream drug manufacturers and downstream insurance companies. They design formularies (lists of drugs that insurance will cover)...

9 3 points 03:02:45 Skipped Javon Company set standards of 2 hours of direct labor per unit at a rate of $15.10 per hour. During October, the company actually uses 11,000 hours of direct labor at a...

Exeter Division of Wetherby Labs acquired an asset with a cost of $800,000 and a four-year life. The cash flows from the asset, considering the effects of Inflation, were scheduled as follows: Year 1...

Flyaway Rural Airlines is planning to add the following three aitcraft to its fleet, an Airbus, a Boeing and an fimbraer, with the following characteristic: Part A: Calculate the weighted average...

A C D E G H 1 The finacial manager of a company is preparing the monthly budget report. He aims to understand which of expenses have been over budget in the previous year. 2 You are required to: 3...

High Country, Incorporated, produces and sells many recreational products. The company has just opened a new plant to produce a folding camp cot that will be marketed throughout the United States....

A liquid flows upward through a valve situated in a vertical pipe. Calculate the differential pressure (kPa) between points A and B. The mean velocity of the flow is 4.1 m/s. The specific gravity of...

Let (x) := x|cos(/x)| for x [0, 1] and let (0+ := 0. Then is continuous on [0, 1] and (x) exists for x E1 := {0} {ak : k N}, where ak := 2/(2k + 1). Let (x) := (x) for x E and (x) := 0 for x ...

Let f be continuous on [a, b], let f(x) > 0 for x [a, b], and let Mn :(ba fn)1/n. Show that lim (Mn) = sup{f(x) : x [a, b]g.

Show that a nonempty finite set S R contains its supremum. [Use Mathematical Induction and the preceding exercise.]

Bach Photographs takes school pictures and charges only $0.99 for a sitting, which consists of six poses. The company then makes up three packages that are offered to the parents, who have a choice...

VERCOR provides merger and acquisition consultants to assist corporations when owners decide to offer their business for sale. One of its news releases, Tax Audit Frequency Is Rising, written by...

The roll of a pair of dice has the following probability distribution, where the random variable x is the sum of the values produced by each die: x P(x) 21/36 32/36 4...3/36 5...4/36 6...5/36...