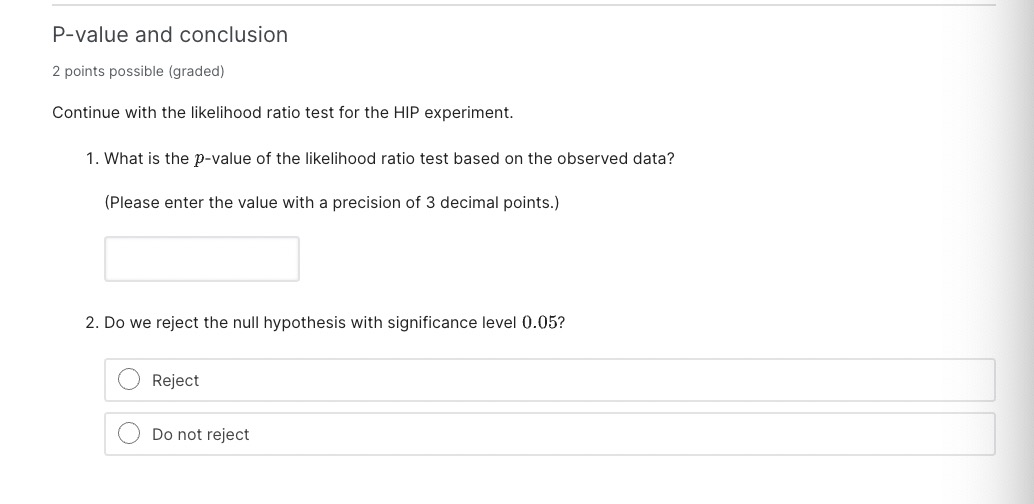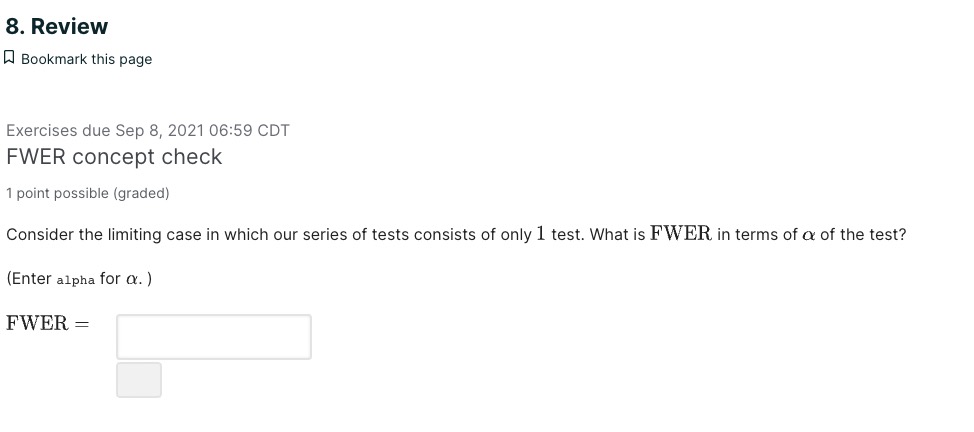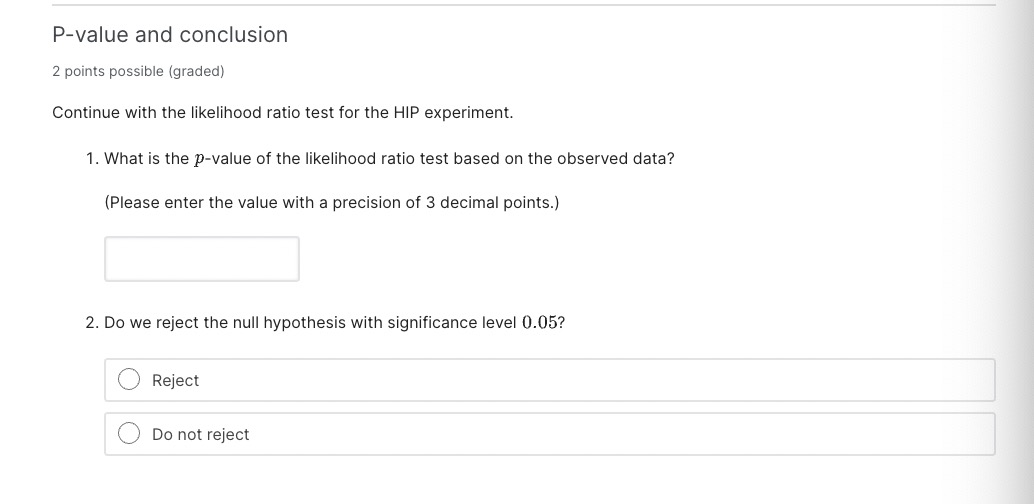







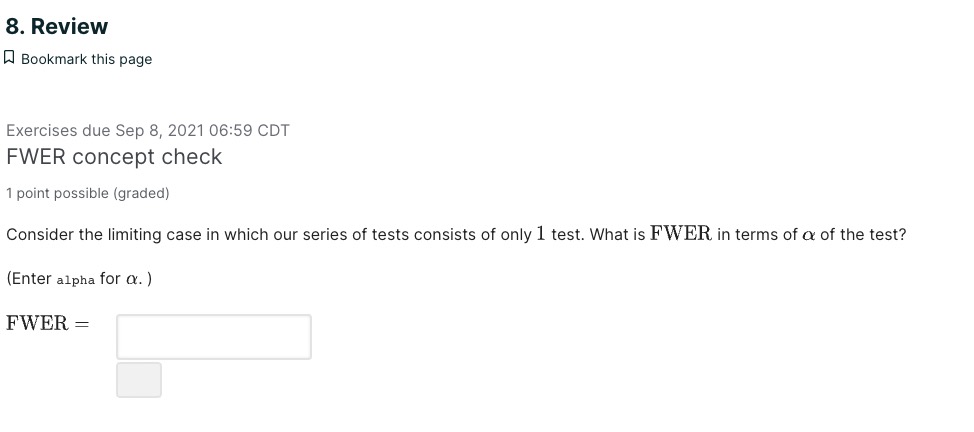
Likelihood ratio test The likelihood ratio test can be applied to a general setting with - Hypotheses: H0 : 9 E 90, HA : (9 6 8A. where 80 and 8A are disjoint subsets (80 F) 9A = 0) of a parameter space 8 : 80 U 9A- - Parametric model with parameter 6: The probability {or likelihood) of observing the data a: isp (3:; 6).with the parameter 6. The likelihood ratio test statistic A (:5) is defined as (negative twice) the logarithm of the likelihood ratio L (3:): maxieec. P (93; 9) A(a:) = 2log(L(m)) wherele) = mgeepm-s) {Equivalently, in the language of maximum likelihood estimators , A constrained P (:3; 9 MILE ) L (w) = , P (9'; 9MLE) A . ' _ _ ' Aconstrained . . _ _ . _ where QMLE is the maXImum likelihood estimator of 6 and aMLE is the constrained maXImum likelihood estimator of 9 within 80.) Likelihood Ratio Test Intuition 2 points possible [graded] Use the definition of likelihood ratio L (at) and the likehood ratio test statistic A (:13) above. We expect the null hypothesis to not be true if {Choose one per column.) OL(X)w1 OA(X)m0 O L(X) xi where d = dim (6) d.im (00) where d is the degree of freedom of the X2 distribution. Power of Likelihood Ratio Test The Neyman-Pearson lemma states that among all tests that test for the simple hypotheses H0 : 9 = 90 ; HA : r9 = 9A at significance level a, the likelihood ratio test is the most powerful. That is, among all tests testing the same simple hypotheses and at the same significance level, the likelihood ratio test gives the largest probability of rejecting the null when indeed the alternate is true. Wilk's Theorem 2 points possible [graded] Given the hypotheses H0 :3260;HA : 6%60, where 9 is a scalar (it takes values from some subset of the Reals}. What is the approximate distribution of the LR-test statistic A (as) when the sample size is large? O t-distribution O X2 -distribution 0 Normal distribution What is the degrees of freedom 01 of the distribution? (If the degrees of freedom doesn't apply, enter -1.) d: In the following problems, we apply the likelihood ratio test to the mammography study to answer the question whether the treatment changes the death rate. The corresponding hypotheses in terms of the breast cancer death rates, Tl'T in the treatment group and fro in the control group, are Parameter Spaces 2 points possible [graded] What is the parameter spaces 80 and (\"3A corresponding to the H0 and HA? Recall that the breast cancer death rate TFT is the probability of an individual in the treatment group dying of breast cancer, and similarly for arc. {Choose any correct answer.) 0 90 :{(7TT17TC) E [0,00) > 1) = P(Vien {V; = 1}) [P( Ti =1) = = m - La. where V is number of tests reported to be significant among all tests with true null hypotheses. I'; is test i, so that I; = 1 corresponds to H; rejected To = {i = 1... m|H; true} is the set of all indices i such that test i has a true null hypothesis Ho mo is the size of To HideHoIm-Bonferroni Correction The Holm-Bonferroni method makes adaptive adjustments to the rejection criterion of each test. The procedure is as follows. Suppose we are testing for m. hypotheses. - Sort the m p-values in increasing orderpm g pm 5 . . . 5 pm >m provided that i 1) FDR = FWER. Now consider the general case when some null hypotheses may be false. This time, when N > 0, we only know that V/M1 1) when V 2 1 V = 1(V>1) =0 when V = 0 Taking expectation on both sides, we see 1)] = P(V 21) FDR FWER. Since FDR is less than FWER, it is easier to control than FWER. That is, we do need to apply as large a correction factor for the FDR than we do to the FWER to get it under our significance threshold o. Therefore, the power of a series of tests with FDR controlled will be larger that the power of the series with FWER controlled FDR Exercise 3 points possible (graded) Use intuition to match the appropriate correction with applications. Every option is only used in one scenario. 1. When generating hypotheses, how should we process p-values? No correction, report the original p-values, but report number of tests performed. FDR