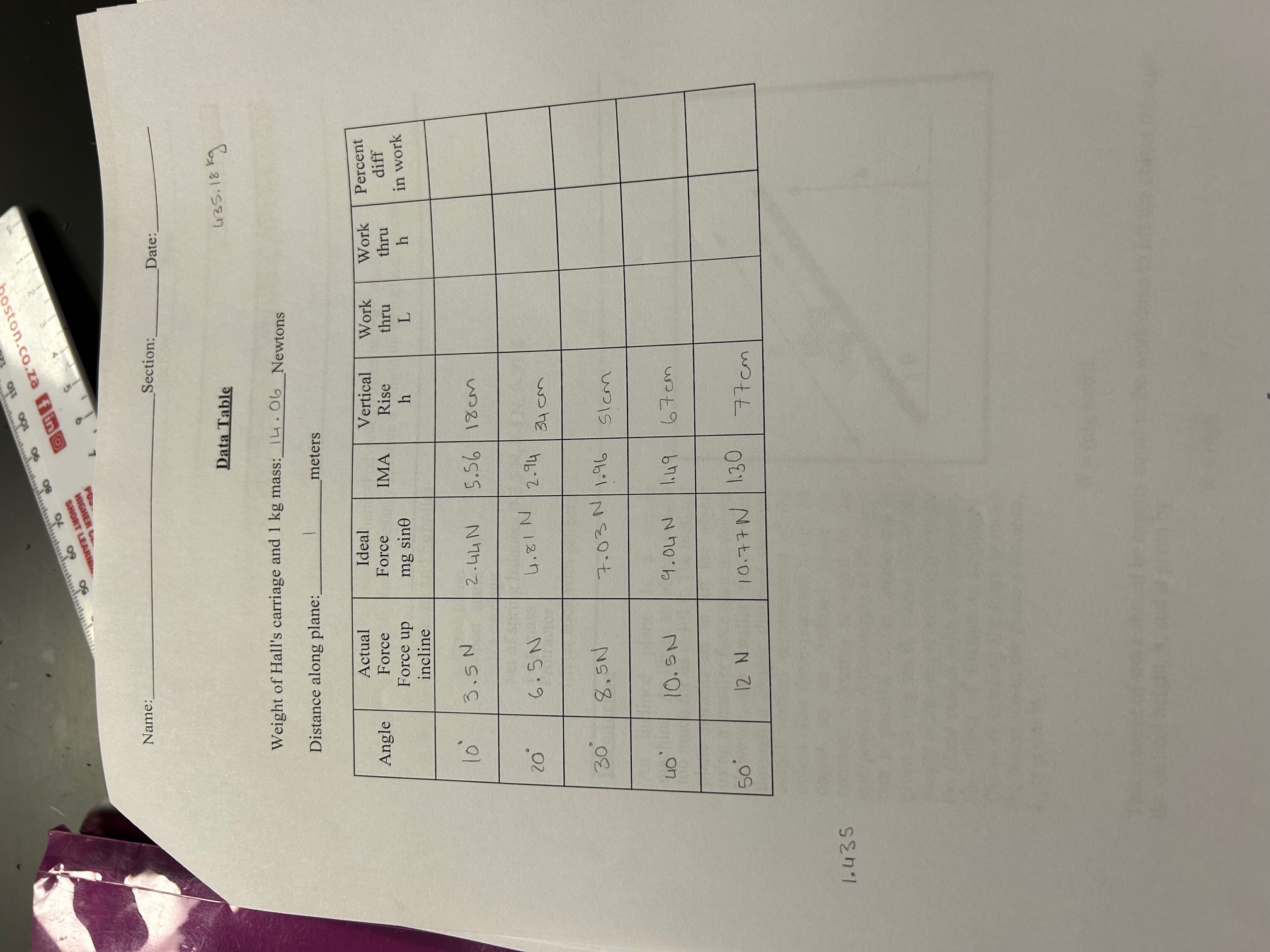
Objectives WORK AND ENERGY 1) To determine the ideal mechanical advantage of an inclined plane. 2) To determine the work necessary to move a weight up an inclined plane. Required Equipment and Supplies Inclined plane Support stand Hall's carriage Set of spring balances 0-2.5 N, 0-5 N, 0-20 N 1-kg mass Protractor Meter stick with calipers Introduction An inclined plane is a simple machine. At times an object weighs too much for us to lift it. The inclined plane permits us to lift the object using a smaller force than its weight. However, the smaller force travels through a longer distance than the actual vertical displacement of the object. The force required to pull an object up an inclined plane (at constant velocity) is equal to the component of the weight of the object that is parallel to the plane and is given by mg sin 0, where mg is the weight of the object and 0 is the angle the plane makes with the horizontal. The effect of friction is neglected. The work done by the force to move the object along the plane a distance, L, is given by L h 0 C W = (mg sin0)L This amount of work should be exactly equal to the work done to lift the object through the vertical height, h, and is given by W = mgh h=18cm l= Imeter 20 30 40 50 Name: Section: Date: The inclined-plane principle is applied in the use of ramps, stairs, screws, escalators, and wedges. Procedures 1) Determine and record the weight of the Hall's carriage. 2) Calculate and record the weight of the Hall's carriage with the 1 kg mass. 3) Set the inclined plane at 10. If you have questions concerning the use of the protrac- tor, ask the instructor before you proceed. 4) Mark the plane to show a starting and an ending point that are 1 meter apart. The carriage will be moving between these two points. 5) Determine the vertical rise between the two end points of the distance L along the incline plane. Record this vertical rise in the data table. 6) Put the 1 kg mass in the Hall's carriage and pull the system up the inclined plane using a spring balance. Record the spring balance reading as the force along the plane. 7) Increase the angle by increments of 10 (up to 50) and repeat step 3. Keep the dis- tance along the plane constant as one meter, but be sure to record the vertical height each time since it will be different. Calculations 1) Calculate the ideal force up the plane, F record in the data table. (1.435) (9.8) Sin (10) = mg sin 0, for each of the five angles and dr fit of eu elitonoq saciq lusine Isuse 2) Determine the IMA (ideal mechanical advantage) of the plane for each of the five angles. Use the Ideal Force calculated in question 1). Show below exactly how you make this determination. (1.435 ) (9.8) (1.435 in (10) = 5.76 3) Calculate the actual work done by the spring scale as you pulled the load up the plane. This is performed by multiplying the Force up the plane by the distance L 2 mim 10 20 Name: Section: Date: 4) Calculate the work needed to lift the load vertically through each of the five heights. 5) Calculate the percent difference between the work thru the distance L and the work thru the distance h. all gripts show nielako yoyob wollt Questions 1) If the IMA can be expressed as the weight (mg) divided by the ideal force up the plane (mg sin 0) gnols show sill mg IMA = mg sine Reduce this ratio to its lowest term and comment on your results. 2) The IMA can also be expressed as the distance up the plane, L, divided by the vertical height, h. 3 Name: 50 60 70 A CONS L IMA = h Section: Date:_ Show that this ratio is the same as the reduced ratio determined in question 1). 3) Using the findings of questions 1) and 2), calculate the IMA for an angle of 18? Calculate the IMA for an angle of 64? 4) How do you explain any differences in the work along the plane and the work through the vertical height? 5) Why should the work along the plane be the same as the work through the vertical height? 4 AMI 1.435 Name: 50 60 80 90 70 100 110 - Data Table Section: Date: Weight of Hall's carriage and 1 kg mass: 14.06 Newtons Distance along plane:_ meters 435.18kg Angle Actual Force Force up incline Ideal Vertical Work Work Percent Force IMA Rise thru thru mg sine h L h diff in work 10 3.5 N 2.44 N 5.56 18cm 20 6.5N 4.81 N 2.94 34cm 30 8.5N 7.03 N 1.96 Slcm 40 10.5N 9.04 N 1.49 67cm 50 12 N 10.77 N 1.30 77cm