Part 2 -- Writing a function DEFINITION and showing a TABLE:

• The starter code includes statements that demonstrate how to use math.pi, math.sin() and math.cos(). You will need these tools for this part of the lab exercise.
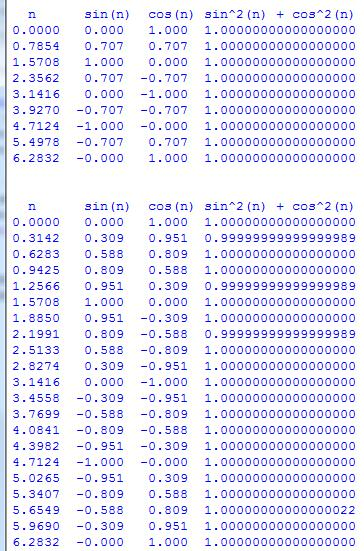
• In a math class you may have learned the following identity: sin²(n) + cos²(n) = 1 for any number 'n' (i.e. "the sin squared plus the cosine squared is equal to one"). In the same file you used for Part 1 above, write code that demonstrates this identity: Write a function definition that takes one parameter named 'intervals', the number of intervals to appear in a table of numbers. The function should print a table with (count+1) rows, showing a sequence of numbers beginning with 0 and ending with 2pi. Each row should also show sin(n), cos(n) and sin²(n) + cos²(n).
• Test your function using the statements provided in the sample code's "main" function (you will need to un-comment the statements when you are ready to use them). Here are the same statements for reference: show_sin_cos_squared_table(8) show_sin_cos_squared_table(20) Here is what the output should look like. Notice when the function is called with the argument 8, the resulting table has 9 rows, with the lowest value of 'n' equal to 0, the highest value (last row) equal to 2pi, and equal steps in the values of 'n'. You can see some representational error in the second table. Notice that the numbers in the last column of the table have 17 digits after the decimal point.

sin (n) cos (n) n^2 (n) + cos*2 (n) 0.0000 000 1.000 1.00000000000000000 0.7854 0.707 0.707 1.00000000000000000 1.5708 1.000 0.000 1.00000000000000000 2.3562 707-0.707 1.00000000000000000 3.1416 0.000-1.000 1.00000000000000000 3.9270 -0.707-0.707 1.00000000000000000 4 . 7124-1, 000-0. 000 1 . 00000000000000000 5.4978 0.707 0.707 1.00000000000000000 6.2832 -0.000 1.000 1.00000000000000000 sin (n) cos (n) n^2 (n) + cos*2 (n) 0.0000 000 1.000 1.00000000000000000 0.3142 0.309 0.951 0.99999999999999989 0.6283 0.588 0.809 1.00000000000000000 0.9425 0.809 0.588 1.00000000000000000 1.2566 0.9510.309 0.99999999999999989 1.5708 1.000 0.000 1.00000000000000000 1.8850 0.951-0.309 1.00000000000000000 2.1991 809-0.588 0.99999999999999989 2.5133 588-0.809 1.00000000000000000 2.8274 0.309-0.951 1.00000000000000000 3.1416 0.000 -1.000 1.00000000000000000 3.4558 -0.309-0.951 1.00000000000000000 3.7699-0.588-0.809 1.00000000000000000 4.0841-0.809 0.588 1.00000000000000000 4 . 3982-0 . 951-0. 309 1 . 00000000000000000 7124 -1.000 -0.000 1.00000000000000000 5.0265 -0.951 0.309 1.00000000000000000 5.3407 -0.809 0.588 1.00000000000000000 5.6549 -0.588 0.809 1.00000000000000022 5.9690 -0.309 .951 1.00000000000000000 6.2832 0.000 1.000 1.00000000000000000 4