*please do in python*

*i have attached my code for the discrete Fourier transform DFT*

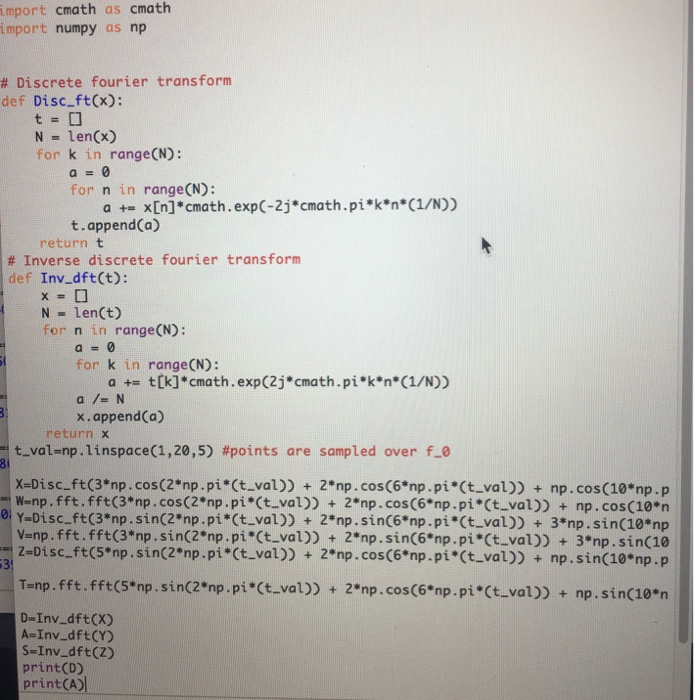
b) Electron wavefunction in momentum space Consider an electron whose 1D spatial wavefunction at t-0 is given by 1 x-5.0 x) = exp Apply your DFT code to obtain the momentum distritution, ie, (p)-Ldery(x). which has an analytic solution. Find this analytic solution, compare to your computational results, and discuss. import ath as cmath import numpy as np # Discrete fourier transform def Disc.ft(x): N len(x) for k in rangeCN): a -0 for n in rangeCN): a += x[n] *cmath . exp(-2j"cmath . pi"k"n"(1/N)) t.append(a) return t # Inverse discrete fourier transform def Inv.dft(t): N len(t) for n in range(N): a=0 for k in rangeCN): a += t(k]*cmath. exp(2j"cmath . pi"k"n"(1/N)) a/= N x. append(a) return x -t-val-np.linspace(1,20,5) #points are sampled over f-0 X-Disc-ft(3*np.cos(2*np.pi*(t val)) 2"np.cos(6*np.pi (t.val)) + np.cos (10*np.p W-np.fft.fft(3*np.cos(2*np.pi (t val)) 2*np.cos (6 np.pi (t val)) + np.cos(10*n Y-Disc-ft("np.sin(2*np.pi"(t-val)) + 2*np .sin(6"np.pi"(t-val)) + 3*np.sin(10" V-np.fft.fft(3"np.sin(2*np.pi (t val)) 2"np.sin(6 np.pi Ct-val)3*np.sin(10 Z-Disc.ft(5 np.sinc2*np.pi (tval)) + 2"np.cos(C6 np.pi (t.val)) + np.sin(10 np.p 3 T-np.fft.fft(5*np. sinc2np.pi Ct-val)) + 2*np.cos(6 np.pi (t-val)) + np.sin(10"n D-Inv dftCX) A-Inv dft() S-Inv dft(Z) print(D) print(A) b) Electron wavefunction in momentum space Consider an electron whose 1D spatial wavefunction at t-0 is given by 1 x-5.0 x) = exp Apply your DFT code to obtain the momentum distritution, ie, (p)-Ldery(x). which has an analytic solution. Find this analytic solution, compare to your computational results, and discuss. import ath as cmath import numpy as np # Discrete fourier transform def Disc.ft(x): N len(x) for k in rangeCN): a -0 for n in rangeCN): a += x[n] *cmath . exp(-2j"cmath . pi"k"n"(1/N)) t.append(a) return t # Inverse discrete fourier transform def Inv.dft(t): N len(t) for n in range(N): a=0 for k in rangeCN): a += t(k]*cmath. exp(2j"cmath . pi"k"n"(1/N)) a/= N x. append(a) return x -t-val-np.linspace(1,20,5) #points are sampled over f-0 X-Disc-ft(3*np.cos(2*np.pi*(t val)) 2"np.cos(6*np.pi (t.val)) + np.cos (10*np.p W-np.fft.fft(3*np.cos(2*np.pi (t val)) 2*np.cos (6 np.pi (t val)) + np.cos(10*n Y-Disc-ft("np.sin(2*np.pi"(t-val)) + 2*np .sin(6"np.pi"(t-val)) + 3*np.sin(10" V-np.fft.fft(3"np.sin(2*np.pi (t val)) 2"np.sin(6 np.pi Ct-val)3*np.sin(10 Z-Disc.ft(5 np.sinc2*np.pi (tval)) + 2"np.cos(C6 np.pi (t.val)) + np.sin(10 np.p 3 T-np.fft.fft(5*np. sinc2np.pi Ct-val)) + 2*np.cos(6 np.pi (t-val)) + np.sin(10"n D-Inv dftCX) A-Inv dft() S-Inv dft(Z) print(D) print(A)