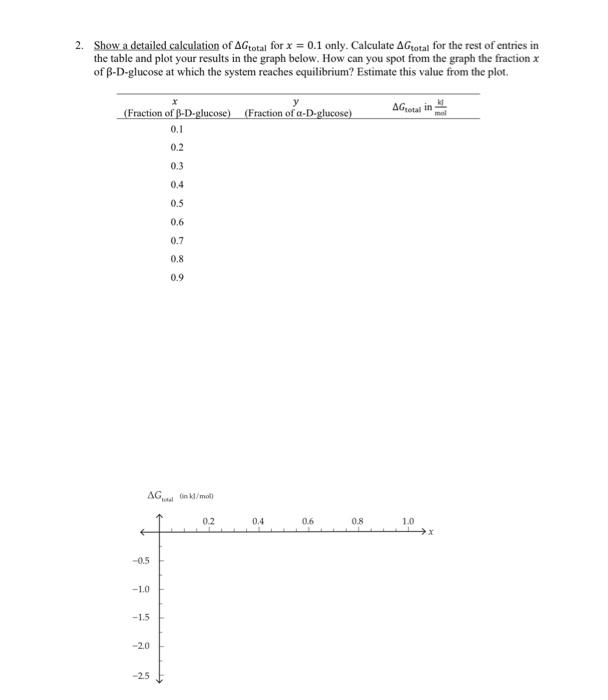
Problem 2: Glucose isomers Glucose can exist in many isomeric forms, In solution, its two most abundant isomers are -D-glucose and -D-glucose. Here you will consider the anomeric conversion of glucose in solution: -D-glucose(aq) -D-glucose(aq). Starting with freshly dissolved -D-glucose as the reactant, the reaction proceeds spontaneously to produce -D-glucose until equilibritum is reached. The multiplicities of both forms are very similar, with -D-glucose having a slightly bigger number of microstates than -D-glucose by a factor of 2528. A. Determine the difference SDSD in entropy (in I/[molK] ) between the D and the D forms. The two forms of glucose have different enthalpies. In fact, the formation of the D form is slightly exothermic as some energy is released as the bonds rearrange. This contributes to the difference in Gibbs free energy between the two, which at 25C is measured to be G=GG=1.43kJ/mol. B. Determine the difference in enthalpy H=HHa (in kJ/mol ) between the two forms at 25C. C. Let's analyze the possibility of equilibrium in this process. As stated above, if 100% of -D-glucose turns into -D-glucose the Gibbs free energy changes by G=GG=1.43kJ/mol. 1. What would be the change in Gibbs free energy if during the conversion only 41 of the glucose ends up as the -D form? What if 43 of it become the -D form? 2. In general, if only a fraction x of the D-glucose ends in solution, what would be the change Ga(x) in Gibbs free energy of the process? Pick a few x values and plot the function. 3. According to your plot, for what fraction x would the Gibbs free energy reach its smallest value? D. We have missed something in this analysis. As more -D-glucose is converted, a different type of entropy change becomes crucial: the entropy of mixing. You derived an expression for this entropy change in Written Homework 4 (for the mixing of two gases, but the result applies equally here); as the -D-glucose and the -D-glucose mix the entropy of the system increases by Smix=NkBxlnxNkBylny where x is the fraction of -D-glucose and y the fraction of -D-glucose in the solution (they add up to 1). Recall that the total number of particles here is N=NA as we are handling quantities "per mol". 1. Determine an improved expression for the "total" Gibbs free energy change Gtoral by adding the effect of this entropy change at 25C to the simple G(x) you found before (Hints: Recall that entropy contributes to G by the term -TS. Also, make sure all terms have the same units!). 2. Show a detailed calculation of Gtotal for x=0.1 only. Calculate Gtotal for the rest of entries in the table and plot your results in the graph below. How can you spot from the graph the fraction x of -D-glucose at which the system reaches equilibrium? Estimate this value from the plot