Prove or disprove that INDEPENDENT-SET ?p SET-PACKING, that is, these two problems are computationally equally hard. Please use an illustration if it helps. The definitions of these two decision problems are summarized below. We already proved that INDEPENDENT-SET ?p SETPACKING, so assume this given.

- INDEPENDENT-SET: Given a graph G = (V, E) and an integer k, is there a subset of vertices 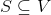such that 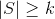and, for each edge in E, at most one - but not both - of its end nodes is in S?

- SET-PACKING: Given a set U of elements, a set of subsets S1, S2, . . . , Sm of U, and an integer k, does there exist a set of at least k subsets that are pairwise disjoint (i.e., intersection = ? between every pair)?

AS C V