Python

Postfix expression used as input and the arithmetic result of the postfix expression processing or error message in case the postfix expression is not correctly rendered. The infix expression used as input. The postfix expression equivalent to the infix expression from #2 or the equivalent postfix expression manually converted and directly entered into your program

infix 3 + 4 16 * 5 7 * 6 + 15 5 + 4 * 2 - 5 (5 + 4) * 2 - 5 24 / 4 + 6 * 2 7 * (6 + 15 11 * 2) + 20 postfix 3 4 + 16 5 * 7 6 * 15 + 5 4 2 * + 5 - 5 4 + 2 * 5 - 24 4 / 6 2 * + 7 6 15 + 11 2 * - * 20 + Postfix expression Input expression in postfix, uses one stack, outputs the arithmetic result

Tokens = numbers (operands or elements), arithmetic operators ({+, -, *, /}), and parentheses Basic algorithm (guaranteed to be mostly correct):

while there are more tokens in the expression read next token

if token is an operand, push token else if token = operator

pop previous two stack elements a then b - error if only one element on stack calculate arithmetic operation using the two elements and operator: b operator a push the result

endwhile

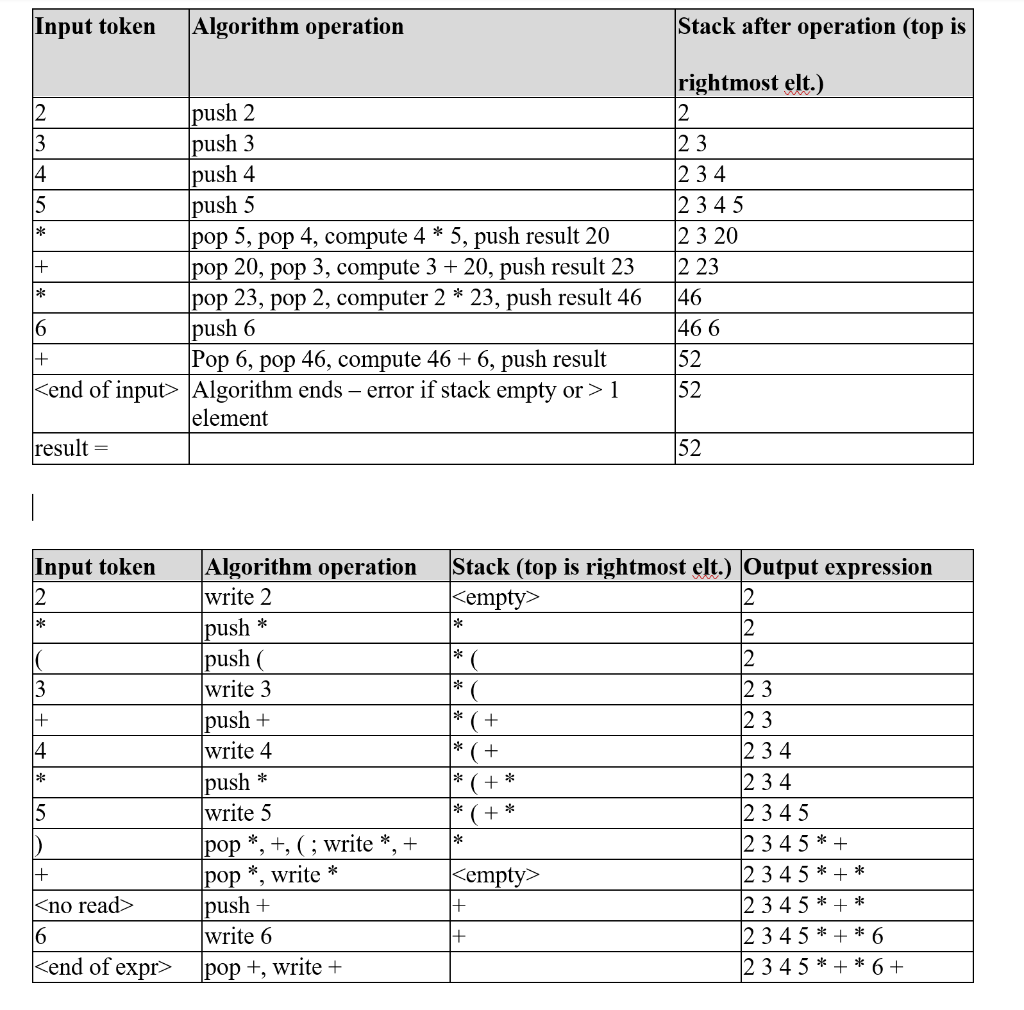
result is the top of stack (and the only element in the stack) error if stack size 1 Example: [2 3 4 5 * + * 6 +] ( = infix expression [2 * (3 + 4 * 5) + 6] )

Infix to postfix expression conversion for use in completing Part 2

Input expression in infix, uses one stack, outputs equivalent postfix expression

Tokens = numbers (operands or elements), arithmetic operators ({+, -, *, /}), and parentheses

Uses one stack, initially empty, with push, pop, top, and empty operations (pop behaves like top-and-

while there are more tokens in the expression read next token

if token is an operand, write it to output else if token =

( : push token

): pop each stack element and write each to output until ( is top, then pop is_an_operator:

if stack is empty or top = ( push token

if operator has higher priority than top, push operator if operator has equal priority to top:

+ or *: push token

/ or -: write top to output, pop, push operator if operator has lower priority than top:

pop and write to output push operator

end else if endwhile

pop and write all remaining stack elements to Output

Example: [2 * (3 + 4 * 5) + 6] [2 3 4 5 * + * 6 +]

\begin{tabular}{|l|l|l|} \hline Input token & Algorithm operation & Stack after operation (top is \\ \hline 2 & rightmost elt.) \\ \hline 3 & push 2 & 2 \\ \hline 4 & push 3 & 23 \\ \hline 5 & push 4 & 234 \\ \hline & push 5 & 2345 \\ \hline+ & pop 5, pop 4, compute 4 5, push result 20 & 2320 \\ \hline & pop 20, pop 3, compute 3+20, push result 23 & 223 \\ \hline 6 & pop 23, pop 2, computer 223, push result 46 & 46 \\ \hline+ & push 6 & 466 \\ \hline & Pop 6, pop 46, compute 46+6, push result & 52 \\ \hline result = & & 52 \\ \hline \end{tabular} \begin{tabular}{|l|l|l|l|} \hline Input token & Algorithm operation & Stack (top is rightmost elt.) & Output expression \\ \hline 2 & write 2 & & 2 \\ \hline & push & & 2 \\ \hline( & push ( & ( & 2 \\ \hline 3 & write 3 & ( & 23 \\ \hline+ & push + & 23 \\ \hline 4 & write 4 & (+ & 234 \\ \hline & push & (+ & 234 \\ \hline 5 & write 5 & 2345 \\ \hline) & pop ,+,(; write ,+ & & 2345+ \\ \hline+ & pop , write & & 2345+ \\ \hline & push + & + & 2345+ \\ \hline 6 & write 6 & 2345+6 \\ \hline & pop +, write + & 2345+6+ \\ \hline \end{tabular}