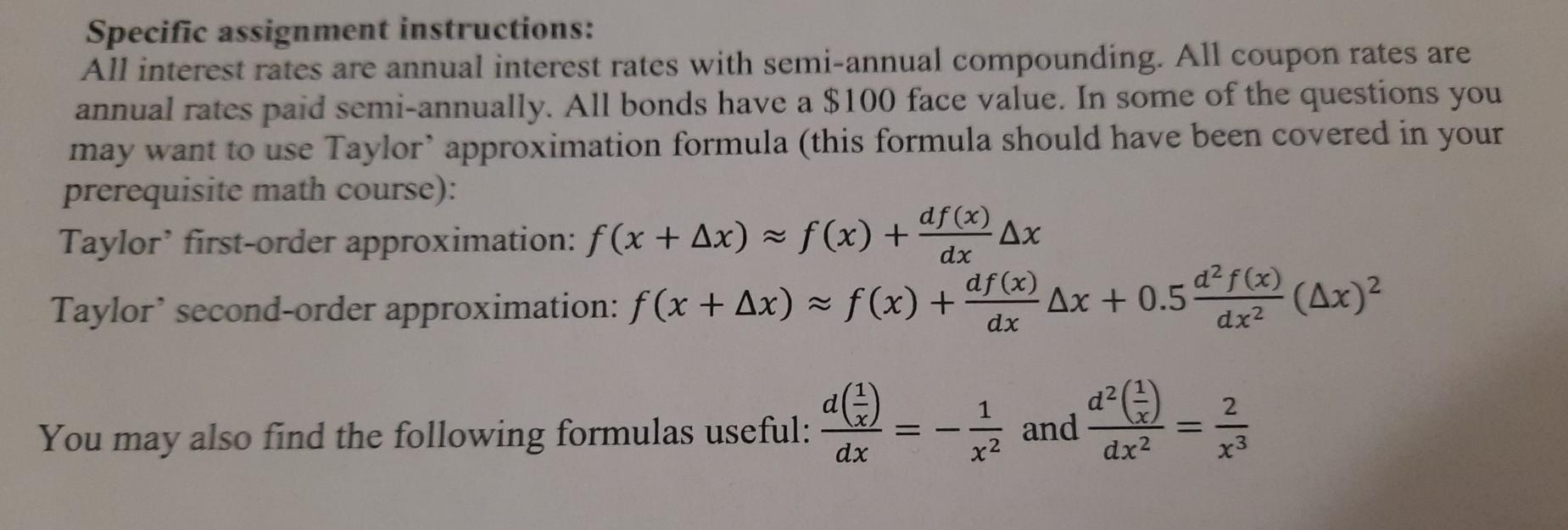
Question 2 only

Specific assignment instructions: All interest rates are annual interest rates with semi-annual compounding. All coupon rates are annual rates paid semi-annually. All bonds have a $100 face value. In some of the questions you may want to use Taylor' approximation formula (this formula should have been covered in your prerequisite math course): df (x) Taylor' first-order approximation: f(x + Ax) f(x) + x df(x) Taylor' second-order approximation: f(x + Ax) = f(x) + (4x) dx Ax +0.5d2f(x) dx dx2 d and dx2 You may also find the following formulas useful: )- 12 13 dx x x3 Problem 1 (10 points): A T-year par rate (T) is the yield to maturity for a par bond (i.e., for a bond with the market price equal to its face value) that matures at time T. Use this definition and assume (0.5) 5% and c(1) 6% a) points) Find a l-year sport rate. Keep at least 6 decimal digits while doing calculations and reporting the answer. b) (3 points) Find the price of a 1-year 7%-coupon bond. Round your answer to the nearest cent. Be very careful with your rounding - an error of $0.01 can lead to a significant penalty. (2 points) Will the YTM on the bond in part (b) be higher or lower than 6%? Either compute this YTM (in which case you need to use a better than 1-cent precision for the bond price) or provide valid reasoning behind your answer. d) (2 points) Assume that future interest rates are known today with 100% certainty (i.e., there is no volatility in future bond prices). Will the capital gain on the bond in part (b) over a 6-month holding period be positive or negative? Explain your reasoning without explicitly computing the future bond price (you may refer to other parameters such as coupon rate, par rates, YTM, etc). Problem 2 (20 points): Consider a 1-factor model with factory. For today's value of y=5%, your portfolio's value is V(0.05)=$1,000,000. However, a small increase in y to y=5.02% will lead to the S5.000 drop in the portfolio's value to V(0.0502)=$995,000, while at y=4.98% your portfolio's value will be V(0.0498)= $1,007,000. a) (6 points) Find DV01, Duration, and Convexity of your portfolio. b) (3 points) Using the first-order Taylor approximation, estimate by how much the value of your portfolio will change when the factor increases to 5.1%. Round your answer to the nearest dollar. c) (3 points) Using the second-order Taylor approximation, estimate by how much the value of your portfolio will change when the factor increases to 5.1%. Round your answer to the nearest dollar. d) (5 points) You would like to use short-term fixed income securities (call them "ST'') with Duration=3 and Convexity=12. What is the dollar value of such securities you need to short? Using the second-order Taylor approximation, by how much the value of your hedged portfolio (in S) will change if y will increase to 5.1%? Round your answers to the nearest dollar. e) (3 points) If, in addition to ST securities in part (d), you can also use long-term fixed income securities (call them "LT") with a Duration=9 and Convexity=80, what will be your best hedging strategy? Specify the dollar value of ST and LT securities you will buy or sell to construct such hedging portfolio. Round your answers to the nearest dollar (note: do not be afraid if your answer will be in hundreds of millions of dollars) Problem 3 (14 points): Assume the term structure of forward rates is flat and they are equal to 5%. The factor y is the forward rate (such one-factor model is called "parallel yield shift" model and in class we called the duration D in this special case by Dmod, i.e., D=Dmod). Assume you own a perpetuity with SIM annual payments paid semi-annually i.e., it pays $500,000 every six months). a) (4 points) Find the current value of this perpetuity, its DV01, Duration, and Convexity. Round your answer to the nearest cent. By how much the value of your perpetuity will change if interest rates increase to y=5.1% (round your answer to the nearest dollar)? b) (5 points) You have decided to hedge your perpetuity using 20-year zero-coupon bonds. How many bonds you should sell (remember that the bond's face value is $100). Round your answer to the nearest integer number of bonds. c) (3 points) Given the hedge you have constructed in part (b), by how much the value of your hedged position will change if interest rates increase to y=5.1%? Use the integer number of bonds from part (b) and round your answers to the nearest dollar. d) (2 points) If, in addition to the 20-year zero-coupon bonds, you would be able to use 5-year zero-coupon bonds, would you be able to construct a better hedge? Explain why (no calculations are necessary). Specific assignment instructions: All interest rates are annual interest rates with semi-annual compounding. All coupon rates are annual rates paid semi-annually. All bonds have a $100 face value. In some of the questions you may want to use Taylor' approximation formula (this formula should have been covered in your prerequisite math course): df (x) Taylor' first-order approximation: f(x + Ax) f(x) + x df(x) Taylor' second-order approximation: f(x + Ax) = f(x) + (4x) dx Ax +0.5d2f(x) dx dx2 d and dx2 You may also find the following formulas useful: )- 12 13 dx x x3 Problem 1 (10 points): A T-year par rate (T) is the yield to maturity for a par bond (i.e., for a bond with the market price equal to its face value) that matures at time T. Use this definition and assume (0.5) 5% and c(1) 6% a) points) Find a l-year sport rate. Keep at least 6 decimal digits while doing calculations and reporting the answer. b) (3 points) Find the price of a 1-year 7%-coupon bond. Round your answer to the nearest cent. Be very careful with your rounding - an error of $0.01 can lead to a significant penalty. (2 points) Will the YTM on the bond in part (b) be higher or lower than 6%? Either compute this YTM (in which case you need to use a better than 1-cent precision for the bond price) or provide valid reasoning behind your answer. d) (2 points) Assume that future interest rates are known today with 100% certainty (i.e., there is no volatility in future bond prices). Will the capital gain on the bond in part (b) over a 6-month holding period be positive or negative? Explain your reasoning without explicitly computing the future bond price (you may refer to other parameters such as coupon rate, par rates, YTM, etc). Problem 2 (20 points): Consider a 1-factor model with factory. For today's value of y=5%, your portfolio's value is V(0.05)=$1,000,000. However, a small increase in y to y=5.02% will lead to the S5.000 drop in the portfolio's value to V(0.0502)=$995,000, while at y=4.98% your portfolio's value will be V(0.0498)= $1,007,000. a) (6 points) Find DV01, Duration, and Convexity of your portfolio. b) (3 points) Using the first-order Taylor approximation, estimate by how much the value of your portfolio will change when the factor increases to 5.1%. Round your answer to the nearest dollar. c) (3 points) Using the second-order Taylor approximation, estimate by how much the value of your portfolio will change when the factor increases to 5.1%. Round your answer to the nearest dollar. d) (5 points) You would like to use short-term fixed income securities (call them "ST'') with Duration=3 and Convexity=12. What is the dollar value of such securities you need to short? Using the second-order Taylor approximation, by how much the value of your hedged portfolio (in S) will change if y will increase to 5.1%? Round your answers to the nearest dollar. e) (3 points) If, in addition to ST securities in part (d), you can also use long-term fixed income securities (call them "LT") with a Duration=9 and Convexity=80, what will be your best hedging strategy? Specify the dollar value of ST and LT securities you will buy or sell to construct such hedging portfolio. Round your answers to the nearest dollar (note: do not be afraid if your answer will be in hundreds of millions of dollars) Problem 3 (14 points): Assume the term structure of forward rates is flat and they are equal to 5%. The factor y is the forward rate (such one-factor model is called "parallel yield shift" model and in class we called the duration D in this special case by Dmod, i.e., D=Dmod). Assume you own a perpetuity with SIM annual payments paid semi-annually i.e., it pays $500,000 every six months). a) (4 points) Find the current value of this perpetuity, its DV01, Duration, and Convexity. Round your answer to the nearest cent. By how much the value of your perpetuity will change if interest rates increase to y=5.1% (round your answer to the nearest dollar)? b) (5 points) You have decided to hedge your perpetuity using 20-year zero-coupon bonds. How many bonds you should sell (remember that the bond's face value is $100). Round your answer to the nearest integer number of bonds. c) (3 points) Given the hedge you have constructed in part (b), by how much the value of your hedged position will change if interest rates increase to y=5.1%? Use the integer number of bonds from part (b) and round your answers to the nearest dollar. d) (2 points) If, in addition to the 20-year zero-coupon bonds, you would be able to use 5-year zero-coupon bonds, would you be able to construct a better hedge? Explain why (no calculations are necessary)