Question
Show that the following three problems are polynomially reducible to each other. (i) Determine, for a given graph G = and a positive integer m
Show that the following three problems are polynomially reducible to each other.
(i) Determine, for a given graph G = 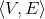 and a positive integer m
and a positive integer m 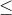
 , whether G contains a clique of size m or more. (A clique of size k in a graph is its complete subgraph of k vertices.)
, whether G contains a clique of size m or more. (A clique of size k in a graph is its complete subgraph of k vertices.)
(ii) Determine, for a given graph G = 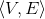 and a positive integer m
and a positive integer m 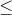
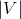 , whether there is a vertex cover of size m or less for G. (A vertex cover of size k for a graph G =
, whether there is a vertex cover of size m or less for G. (A vertex cover of size k for a graph G = 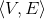 is a subset V'
is a subset V' 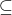 V such that
V such that  = k and, for each edge (u, v)
= k and, for each edge (u, v) 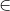 E, at least one of u and v belongs to V'.)
E, at least one of u and v belongs to V'.)
(iii) Determine, for a given graph G = 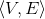 and a positive integer m
and a positive integer m 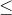
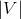 ,whether G contains an independent set of size m or more. (An independent set of size k for a graph G =
,whether G contains an independent set of size m or more. (An independent set of size k for a graph G = 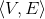 is a subset V'
is a subset V' 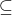 V such that
V such that 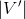 = k and for all u, v
= k and for all u, v 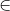 V', vertices u and v are not adjacent in G.)
V', vertices u and v are not adjacent in G.)
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


