Suppose you are given a supply string S[0 . . N ? 1] of period n, which includes symbols a and b. Suppose further that you are given a sample string P[0 . . M ? 1] of duration m n, consisting of symbols a, b, and ?, representing a sample to be located in string S. The image ? is a "wild card" symbol, which fits a unmarried image, both a or b. The different symbols should fit precisely.

The problem is to output a sorted listing M of valid "match positions", which might be positions j in S such that pattern P suits the substring S[j . . J + example, if S = a b a b b a b and P = a b ?, then the output M must be [0, 2].

(a) Describe a honest, na?ve algorithm to clear up the hassle. Your

set of rules should run in time O(nm).

(b) Give an set of rules to solve the trouble with the aid of reducing it to the trouble of polynomial multiplication. Specifically, describe how to convert strings S and P into polynomials such that the manufactured from the polynomials lets in you to determine the solution M. Give examples to illustrate your polynomial representation of the inputs and your way of determining outputs from the product, based totally on the instance S and P strings given above.

(c) Suppose you combine your approach to Part (b) with an FFT algorithm for

polynomial multiplication. What is the time complexity of the resulting approach to the string matching problem?

(d) Now consider the identical problem however with a larger image alphabet. Specifically, think you are given a representation of a DNA strand as a string D[0 . . N?1] of period n, including symbols A, C, G, and T; and you're given a pattern string P[0 . . M ? 1] of length m n, such as symbols A, C, G, T, and ?. The hassle is, again, to output a taken care of list M of legitimate "fit positions", which can be positions j in D such that pattern P fitsPinstance, if D = A C G A C C A T and P = A C ? A, then the output M have to be [0, 3]. Based to your solutions to Parts (b) and (c), provide an efficient set of rules for this placing. Illustrate your algorithm on the example above.

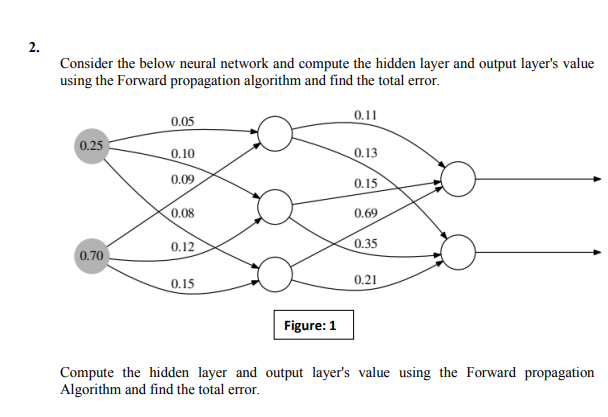
2. Consider the below neural network and compute the hidden layer and output layer's value using the Forward propagation algorithm and find the total error. 0.25 0.70 0.05 0.10 0.09 0.08 0.12 0.15 Figure: 1 0.11 0.13 0.15 0.69 0.35 0.21 Compute the hidden layer and output layer's value using the Forward propagation Algorithm and find the total error.