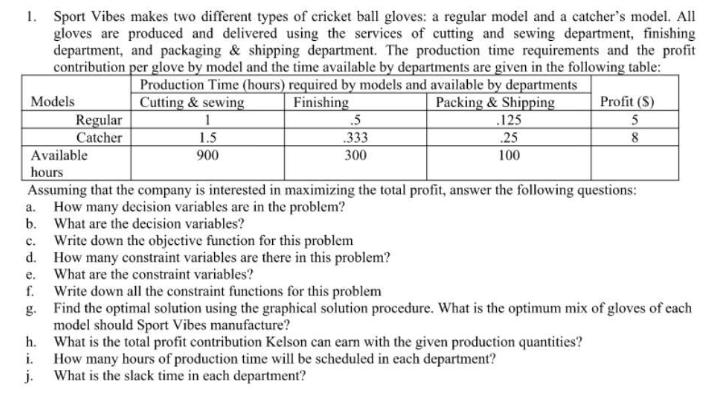
1. Sport Vibes makes two different types of cricket ball gloves: a regular model and a catcher's model. All gloves are produced and delivered using the services of cutting and sewing department, finishing department, and packaging & shipping department. The production time requirements and the profit contribution per glove by model and the time available by departments are given in the following table: Production Time (hours) required by models and available by departments Cutting & sewing Finishing Packing & Shipping Models Regular Catcher 1 1.5 900 h. i. j. .5 .333 300 b. What are the decision variables? C. Write down the objective function for this problem d. How many constraint variables are there in this problem? e. What are the constraint variables? f. g. 125 25 100 Available hours Assuming that the company is interested in maximizing the total profit, answer the following questions: a. How many decision variables are in the problem? Profit (S) 5 8 Write down all the constraint functions for this problem Find the optimal solution using the graphical solution procedure. What is the optimum mix of gloves of each model should Sport Vibes manufacture? What is the total profit contribution Kelson can earn with the given production quantities? How many hours of production time will be scheduled in each department? What is the slack time in each department? 2. Kariba Investments manages funds of several companies and affluent individuals. Kariba devices investment strategy for clients based on each client's needs. For a new client, It has been authorized to invest up to $1.2 million in two investment funds: (i) an active stock fund and (ii) a money market fund. Each unit of the active stock costs $50 and provides an annual rate of return of 10% while each unit of the money market fund costs $100 and provides an annual rate of return of 4%. The client wants to minimize risk subject to the requirement that the annual income from the investment be at least $60,000. According to Kariba's risk measurement system, each unit invested in the active stock has a risk index of 8, and each unit invested in the money market fund has a risk index of 3; the higher risk index associated with the stock fund simply indicates that it is the riskier investment. Kariba's client also specified that at least $300,000 be invested in the money market fund. a. Identify the decision variables. Name the decision variables for mathematical modelling. What are the parameters of the decision variables? Is it an objective maximization or minimization problem? Write the objective function. b. What are the constraint variables? Name the constraint variables. Write the constraints functions c. Determine how many units of each fund Kariba should purchase for the client to minimize the total risk index for the portfolio d. How much annual income will this investment strategy generate? e. Suppose the client desires to maximize annual return. How should the funds be invested? 3. Sonny Electronics manufactures two LCD television monitors, identified as model A and model B. Each model has its lowest possible production cost when produced on Sonny's new production line. However, the new production line does not have the capacity to handle the total production of both models. As a result, at least some of the production must be routed to a higher-cost, old production line. The following table shows the minimum production requirements for next month, the production line capacities in units per month, and the production cost per unit for each production line: Model A B Production Line Capacity Let AN AO BN Production Cost per Unit Old Line New Line $30 $25 80,000 $50 $40 60,000 Minimum Production Requirements 50,000 70,000 Units of model A produced on the new production line Units of model A produced on the old production line Units of model B produced on the new production line BO Units of model B produced on the old production line Sonny's objective is to determine the minimum cost production plan. a. Formulate the linear programming model for this problem using the following four constraints. Clearly write the objective function and the constraints equations: Constraint 1: Minimum production for model A Constraint 2: Minimum production for model B Constraint 3: Capacity of the new production line Constraint 4: Capacity of the old production line b. Using Solver solve the problem. Generate answer report and sensitivity report. c. What is the optimum product mix? what is the total production cost associated with this solution? d. Which constraints are binding? Explain. e. The production manager noted that the only constraint with a positive dual value is the constraint on the capacity of the new production line. The manager's interpretation of the dual value was that a one-unit increase in the right-hand side of this constraint would increase the total production cost by $15 per unit. Do you agree with this interpretation? Would an increase in capacity for the new production line be desirable? Explain. f. Would you recommend increasing the capacity of the old production line? Explain. g. The production cost for model A on the old production line is $50 per unit. How much would this cost have to change to make it worthwhile to produce model A on the old production line? Explain. h. Suppose that the minimum production requirement for model B is reduced from 70,000 units to 60,000. What effect would this change have on the total production cost? Explain. c. The first three constraints are binding because the values in the Slack/Surplus column for these constraints are zero. The fourth constraint, with a slack of 0 is nonbinding. d. The dual price for the new production line capacity constraint is 15. Because the dual price is positive, increasing the right-hand side of constraint 3 will improve the solution. Because the object is to minimize the total production cost, an improvement in the solution corresponds to a reduction in the total production cost. Thus, every one unit increase in the right-hand side of this constraint will actually reduce the total production cost by $15. In other words, an increase in capacity for the new production line is desirable. e. Because constraint 4 is not a binding constraint, any increase in the production line capacity of the old production line will have no effect on the optimal solution. Thus, there is no benefit in increasing the capacity of the old production line. f. The reduced cost for Model A made on the old production line is 5. Thus, the cost would have to decrease by at least $5 before any units of model A would be produced on the old production line. g. The right-hand side range for constraint 2 shows a lower limit of 30,000. Thus, if the minimum production requirement is reduced 10,000 units to 60,000, the dual price of -40 is applicable. Thus, total cost would decrease by 10,000(40) = $400,000.