The goal of this programming assignment is two-fold. The first goal is to observe empirically the complexities of different algorithms solving the same problem. The second goal is to discover how accurate the theoretical estimates of complexity are when compared to real execution times. You can implement the code in C, C++, Java. For other programming languages, please consult with the instructor. In this assignment, you will implement three sorting algorithms: ALG1, ALG2, and ALG3. For the algorithms discusses in class, the implementation should follow exactly the algorithms (pseudocode) learned in class, which is the same as in the textbook. The final submission consists of: Source code A report consisting of:

1. A graph showing a comparison of the running times of the three algorithms for various input sizes (see below for details)

2. Three tables, one for each algorithm, showing a comparison of the actual and theoretical running times. For each algorithm, compute an approximation of the hidden constant in the O-notation More details: Run experiments varying n (where n is the number of elements) from ns to nf, with increment . For each n value, run each algorithm m times on different input arrays and take the average of the running times. Run the three algorithms on the same input arrays. To generate numbers, use a random number generator. Then for each array instance run the algorithms. You can use rand() which generates a random number between 0 and RAND_MAX = 32767. Include #include. Determine the unit of time for your measurements, such as milliseconds (ms) or microseconds (s). For s, if you use unix you can use for example "gettimeofday" which gives the time in sec and microseconds. Use "man gettimeofday" to see the manual description. You need to plot the running time of the algorithms as a function of the number of elements n Approximate the value of the hidden constant in the O-notation by dividing the running times with the theoretical values and then taking the maximum value over all input sizes. Make sure you address the issue with the array indexes! In our classnotes/textbook, we assume arrays start from the index 1, e.g. A[1..n], while in many programming languages arrays start from the index 0, e.g. A[0..n-1].

PSEUDOCODES TO FOLLOW BELOW

ALG 1 INSERTION-SORT PSEUDOCODE

ALG2- HEAP SORT PSEUDO CODE

_______________________________

ALG3- QUICK SORT PSEDUOCODE

___________________________________

MORE EXPLANATION FOR THE ASSIGNMENT ITSELF

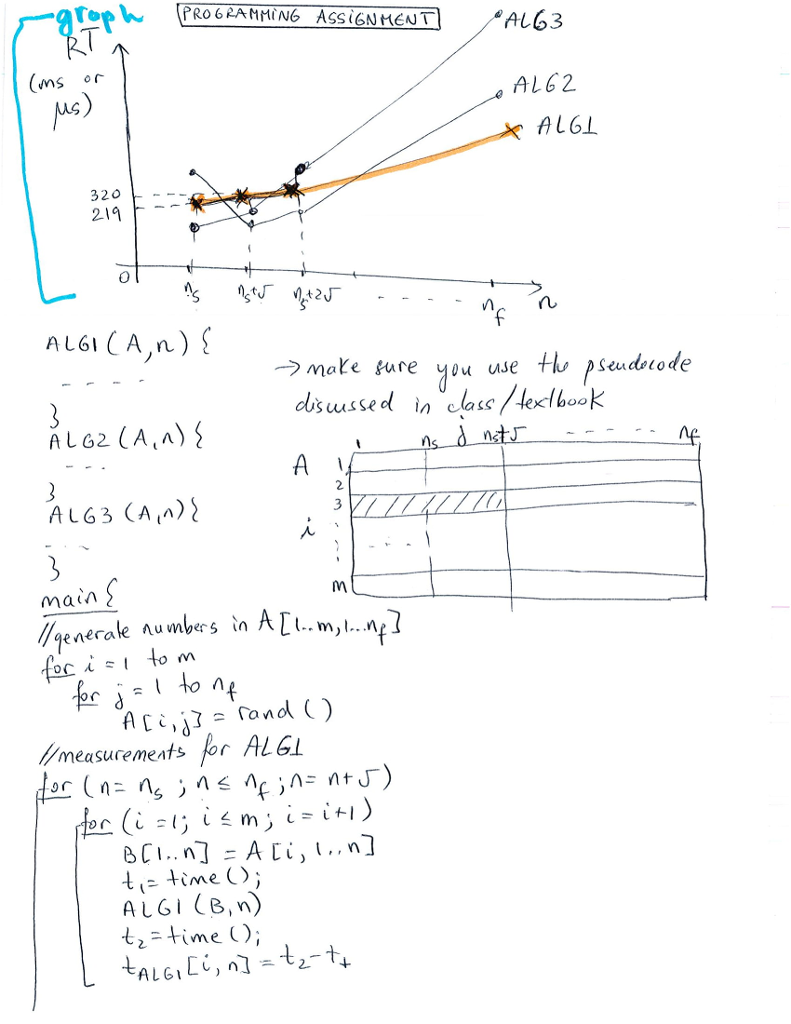
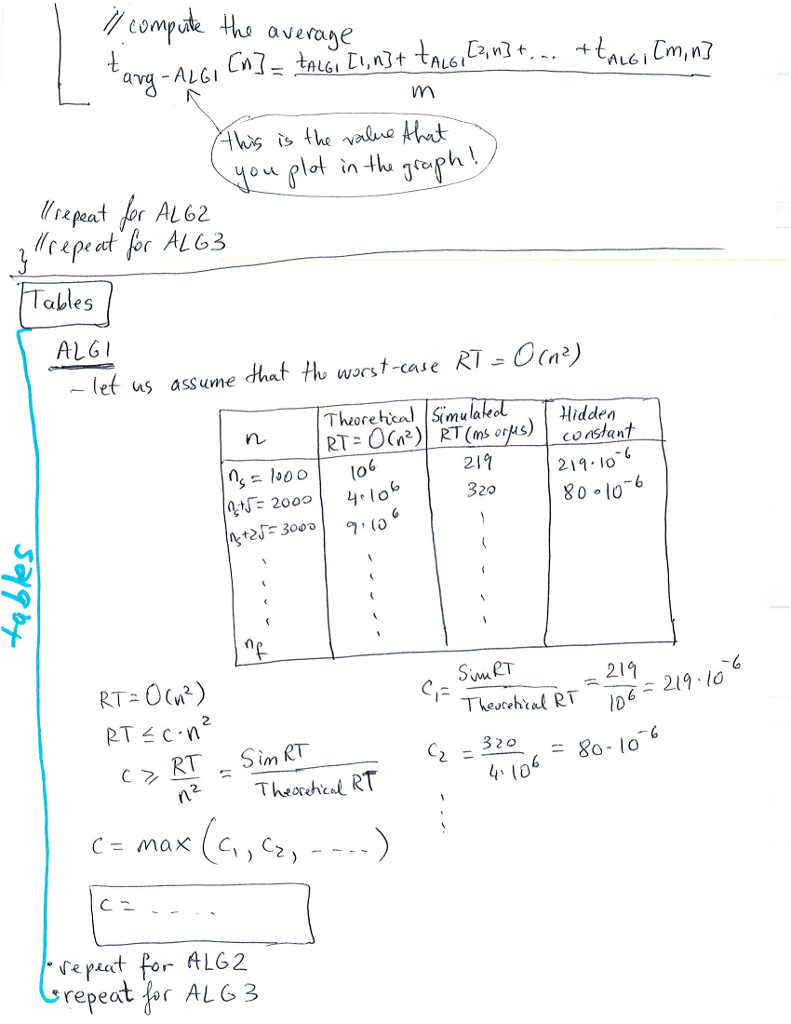
For this programming assignment, use the following specifications: ALG1 = INSERTION-SORT

ALG2 = HEAP-SORT

ALG3 = QUICKSORT

ns = 1000

nf = 20000

= 1000

m = 10

Desinang and Analysing Algoritms. Insertion sort alaorith The Sor tiwg Problem Outpud, a per mutation Cor reorder tny) of the numbers in : well-depined eomputahonal procedure fhat or set of values) as input and produces a value or set of values) as outpuit Dala strudure s provide a way to soe ud ogeie data cperations used to access and mo dipy daa The Insertion ort algorithm Cost imes Key =AGJ n-I n-I n-l 2 nSer Sor wbile io and A Ci k nu 5 1-1 n-l