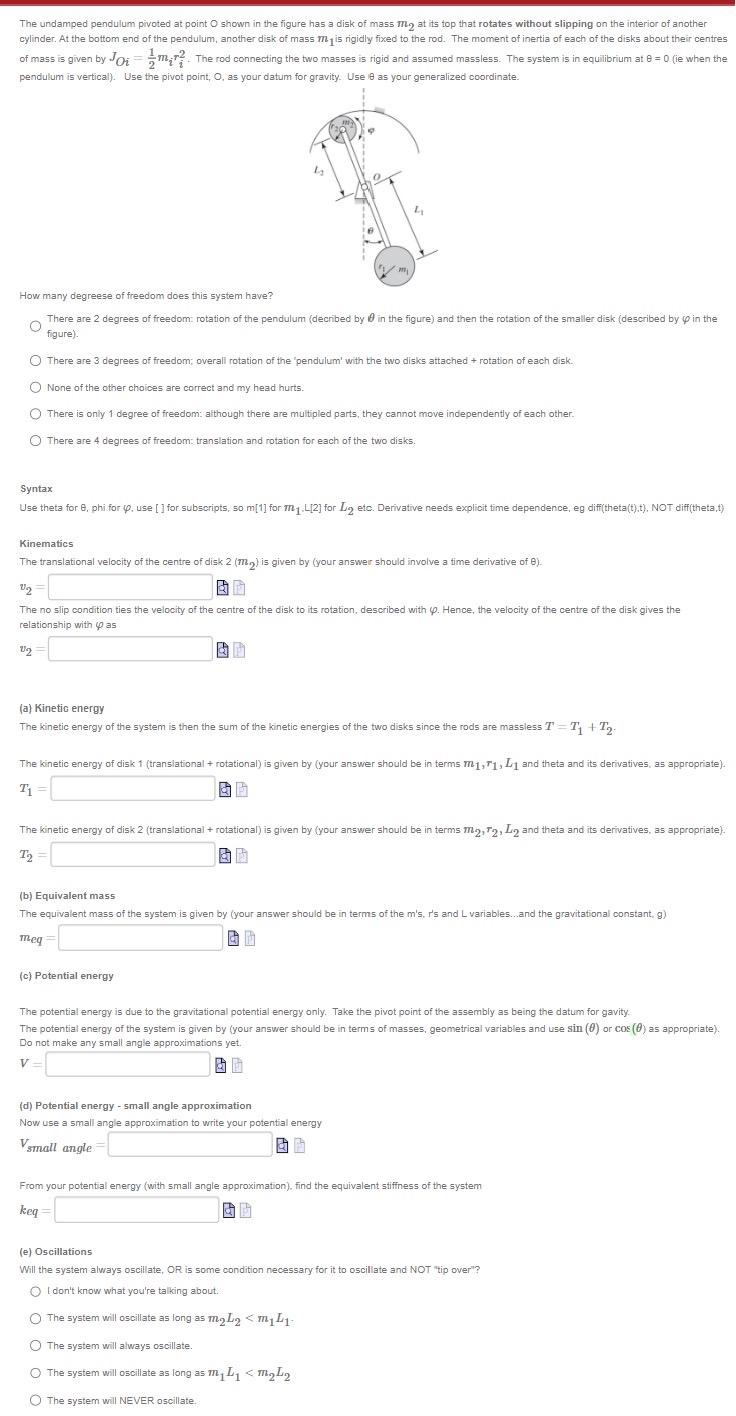
The undamped pendulum pivoted at point O shown in the figure has a disk of mass m2 at its top that rotates without slipping on the interior of another cylinder. At the bottom end of the pendulum, another disk of mass mis rigidly fixed to the rod. The moment of inertia of each of the disks about their centres of mass is given by Joim. The rod connecting the two masses is rigid and assumed massless. The system is in equilibrium at 8 = 0 (ie when the pendulum is vertical). Use the pivot point, O, as your datum for gravity. Use 8 as your generalized coordinate. b U2 O How many degreese of freedom does this system have? O There are 2 degrees of freedom: rotation of the pendulum (decribed by in the figure) and then the rotation of the smaller disk (described by in the figure). O There are 3 degrees of freedom; overall rotation of the 'pendulum' with the two disks attached + rotation of each disk. None of the other choices are correct and my head hurts. O There is only 1 degree of freedom: although there are multipled parts, they cannot move independently of each other. O There are 4 degrees of freedom: translation and rotation for each of the two disks. my Syntax Use theta for 8, phi for p. use [] for subscripts, so m[1] for m.L[2] for Lq etc. Derivative needs explicit time dependence, eg diff(theta(t).t), NOT diff(theta,t) 2 Kinematics The translational velocity of the centre of disk 2 (m) is given by (your answer should involve a time derivative of 8). V The no slip condition ties the velocity of the centre of the disk to its rotation, described with p. Hence, the velocity of the centre of the disk gives the relationship with pas (a) Kinetic energy The kinetic energy of the system is then the sum of the kinetic energies of the two disks since the rods are massless T=T+T2. (c) Potential energy The kinetic energy of disk 1 (translational + rotational) is given by (your answer should be in terms m1,71, L1 and theta and its derivatives, as appropriate). T & G The kinetic energy of disk 2 (translational + rotational) is given by (your answer should be in terms m2, 72, L2 and theta and its derivatives, as appropriate). T2 (b) Equivalent mass The equivalent mass of the system is given by (your answer should be in terms of the m's, r's and L variables...and the gravitational constant, g) meq (d) Potential energy - small angle approximation Now use a small angle approximation to write your potential energy Vsmall angle The potential energy is due to the gravitational potential energy only. Take the pivot point of the assembly as being the datum for gavity. The potential energy of the system is given by (your answer should be in terms of masses, geometrical variables and use sin (0) or cos (0) as appropriate). Do not make any small angle approximations yet. V= From your potential energy (with small angle approximation), find the equivalent stiffness of the system keq (e) Oscillations Will the system always oscillate, OR is some condition necessary for it to oscillate and NOT "tip over"? O I don't know what you're talking about. O The system will oscillate as long as mL2