This is a java code problem using eclipse, there are two codes below.

The purpose is to work the BinaryTreeTest code, and get a score of 100.

CODE Below:

import java.util.Arrays;

/** * A binary search tree for Comparable objects such as Strings, Integers, etc. * For each node n, all nodes to the left have data which is less than n.data * and all nodes to the right have data which is greater than n.data. * * @param */ public class BinaryTree> { private static class Node> { public T data; public Node left, right;

public void add(T d) { int comp = d.compareTo(data); if (comp == 0) return; // Already in tree if (comp (); left.data = d; } else { left.add(d); } } else { // Greater than if (right == null) { right = new Node(); right.data = d; } else { right.add(d); } } }

public boolean contains(T d) { int comp = d.compareTo(data); if (comp == 0) return true; // Already in tree if (comp

}

public void print(int indent) { if (right != null) right.print(indent + 1); char[] spaces = new char[indent * 2]; Arrays.fill(spaces, ' '); System.out.println(new String(spaces) + data); if (left != null) left.print(indent + 1); }

/** * The number of nodes of this subtree. * @return Number of nodes */ public int size() { // We know there is a node here int total = 1; // This node may have left children if (left != null) total = total + left.size(); // This node may have right children if (right != null) total = total + right.size(); // The total size of the tree from this point... return total; }

/** * Delete this node. * * @return The new root of this subtree (null if this node had no * children, also known as a leaf) */ public Node deleteNode() { if (left == null) return right; if (right == null) return left; Node successor = right; if (successor.left == null) { // Case 1: no left child of immediate successor right = right.right; } else { // Case 2: loop until we find leftmost child Node successorParent = null; while (successor.left != null) { successorParent = successor; successor = successor.left; } successorParent.left = successor.right; } // Replace this data with successor data data = successor.data; return this; }

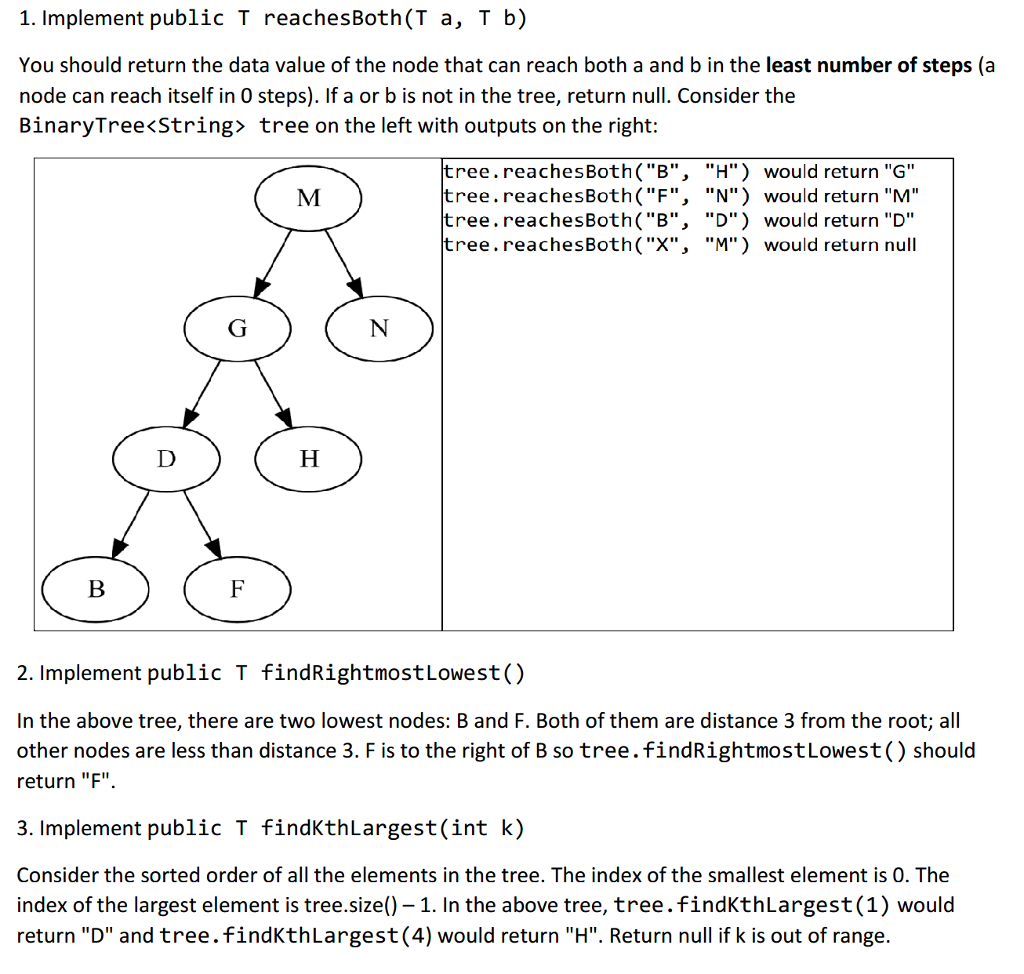
/** * Deletes the node containing d if it exists. * * @param d * @return A valid BinaryTree that doesn't have d in it but does have * everything else. */ public Node delete(T d) { int comp = d.compareTo(data); if (comp == 0) return deleteNode(); if (comp

private Node root;

public BinaryTree() { root = null; }

/** * Adds data to the tree if it didn't already contain it. * * @param data */ public void add(T data) { if (root == null) { root = new Node(); root.data = data; } else { root.add(data); } }

/** * Returns true if the tree contains data, false otherwise * * @param data * Does the tree contain this? * @return true if it does */ public boolean contains(T data) { if (root == null) return false; return root.contains(data); }

/** * Prints out a representation of the tree (rotate your head 90 degrees * left) */ public void print() { if (root != null) root.print(0); }

/** * Gets the number of nodes of the tree in O(n) time. * * @return number of nodes */ public int size() { if (root == null) return 0; return root.size(); }

/** * Delete the node containing data from the tree, if it exists. * * @param data */ public void delete(T data) { root = root.delete(data); }

/** * Returns the data value of the node that can reach both a and b in the * least number of steps. If the tree doesn't contain both a and b, return * null. * * @param a * @param b * @return data value */ public T reachesBoth(T a, T b) { // TODO: Implement. return null; }

/** * Among all the nodes which are farthest from the root, find the one which * is farthest to the right. * * @return data value of said node */ public T findRightmostLowest() { // TODO: Implement. return null; }

/** * Return the kth largest element according to the Comparable sorted order * of the tree. The leftmost node has index 0 and the rightmost node has * index size() - 1. * * @param k * index * @return element, or null if k is out of range. */ public T findKthLargest(int k) { // TODO: Implement. return null; }

/** * EXTRA CREDIT: Balance the tree. The new root should be the * findKthLargest(size()/2) node. Recursively, the root of each subtree * should also be the size/2-largest node (indexed from 0) of that subtree. * This method should not call new and should execute in O(n log n) time for * full credit. */ public void balance() { // TODO: Implement for extra credit. } }

TEST CODE Below:

import java.io.ByteArrayOutputStream; import java.io.PrintStream; import java.security.MessageDigest; import java.security.NoSuchAlgorithmException; import java.util.Arrays;

public class BinaryTreeTest {

public static > int reachScore(BinaryTree tree, String name, T first, T second, T correct, int score) { if (first instanceof String) { System.out.println("Testing " + name + ".reachesBoth(\"" + first + "\", \"" + second + "\")"); } else { System.out.println("Testing " + name + ".reachesBoth(" + first + ", " + second + ")"); } T rb = tree.reachesBoth(first, second); if (correct == rb || (correct != null && correct.equals(rb))) { System.out.println("Got correct value of " + rb); return score; } else { System.out.println("Expected " + correct + " got " + rb); return 0; } }

public static > int rightmostLowestScore(BinaryTree tree, String name, T correct, int score) { System.out.println("Testing " + name + ".findRightmostLowest()"); T rb = tree.findRightmostLowest(); if (correct == rb || (correct != null && correct.equals(rb))) { System.out.println("Got correct value of " + rb); return score; } else { System.out.println("Expected " + correct + " got " + rb); return 0; } }

public static > int kthLargestScore(BinaryTree tree, String name, int k, T correct, int score) { System.out.println("Testing " + name + ".findKthLargest(" + k + ")"); T rb = tree.findKthLargest(k); if (correct == rb || (correct != null && correct.equals(rb))) { System.out.println("Got correct value of " + rb); return score; } else { System.out.println("Expected " + correct + " got " + rb); return 0; } }

public static void main(String[] args) throws NoSuchAlgorithmException { int reachesBothScore = 0, findRightmostLowestScore = 0, findKthLargestScore = 0; int ecScore = 0; try { String[] letters = { "M", "G", "N", "D", "H", "B", "F" }; BinaryTree letterTree = new BinaryTree(); for (String name : letters) { letterTree.add(name); } BinaryTree emptyTree = new BinaryTree(); BinaryTree simpleTree = new BinaryTree(); simpleTree.add("Hello"); reachesBothScore += reachScore(letterTree, "letterTree", "B", "H", "G", 2); reachesBothScore += reachScore(letterTree, "letterTree", "F", "N", "M", 2); reachesBothScore += reachScore(letterTree, "letterTree", "B", "D", "D", 2); reachesBothScore += reachScore(letterTree, "letterTree", "X", "M", null, 2); reachesBothScore += reachScore(letterTree, "letterTree", "N", "N", "N", 2); reachesBothScore += reachScore(emptyTree, "emptyTree", "a", "b", null, 2); findRightmostLowestScore += rightmostLowestScore(letterTree, "letterTree", "F", 2); findRightmostLowestScore += rightmostLowestScore(simpleTree, "simpleTree", "Hello", 2); findKthLargestScore += kthLargestScore(letterTree, "letterTree", 1, "D", 2); findKthLargestScore += kthLargestScore(letterTree, "letterTree", 4, "H", 2); findKthLargestScore += kthLargestScore(letterTree, "letterTree", -1, null, 2); findKthLargestScore += kthLargestScore(letterTree, "letterTree", 7, null, 2); letterTree.add("P"); findRightmostLowestScore += rightmostLowestScore(letterTree, "letterTree", "F", 2); letterTree.add("O"); findRightmostLowestScore += rightmostLowestScore(letterTree, "letterTree", "O", 2);

BinaryTree intTree = new BinaryTree(); int[] rightLow = { 1, -56981709, -113963419, -95375583, -95375583, -105278602, -86690766, -86690766, -96593785, -96593785 }; Integer[] kthLarge = { null, 2081208021, 47078692, -652853260, -1078997883, -1277215666, -1410985124, -1524948544, -1590615071, -1667402819 }; for (int i = 1, j = 0; j 0) System.out.println("Extra credit: "+ecScore+" out of 2 examples got expected result (not a final score)"); else System.out.println("You may want to work on the extra credit!"); System.out.println("Score may be affected by academic honesty policy."); } }

}

1. Implement public T reachesBoth(T a, T b) You should return the data value of the node that can reach both a and b in the least number of steps (a node can reach itself in 0 steps). If a or b is not in the tree, return null. Consider the Binary Tree String> tree on the left with outputs on the right: tree reaches Both ("B", "H") would return "G tree reaches Both ("F", "N") would return "M" M tree reaches Both("B" D") would return "D tree. reaches Both("X", "M") would return null 2. Implement public T findRightmostLowest() n the above tree, there are two lowest nodes: B and F. Both of them are distance 3 from the root; all other nodes are less than distance 3. F is to the right of B so tree. findRightmostLowest() should return "F" 3. Implement public T findKthLargest(int k) Consider the sorted order of all the elements in the tree. The index of the smallest element is 0. The index of the largest element is tree.size()-1. In the above tree, tree. findKthLargest(1) would return "D" and tree find thLargest (4) would return "H". Return null if k is out of range