Title: Java-receive infix exp. Give & eval prefix,postfix exp using Queue & Stack.

Use psuedocode provided .Provide your own generic Queue & Stack(I did) to receive an infix from user, give postfix exp, prefix exp, and eval postfix, prefix.

Use described methods to implement your Queue & Stack. User input should be received as a string and then tokenized into char.

No input validation is needed here. Assume the user will only enter single digit numbers and no floats. Also assume the user will only enter valid operators along with parentheses (if desired). No spaces are allowed in the input so you can safely assume no spaces are in the input. The valid operators you must handle are: + (addition), - (subtraction), / (integer division), * (multiplication), and ^ (exponentiation).

Here are some sample outputs. Your output and prompts should look like this

$ javac Main.java $ java Main Enter infix expression: 3*4-(7-8/2)

Postfix: 34*782/- Result: 9

Prefix: -*34-7/82 Result: 9

Methods to be implemented

Methods to be implemented

----public static void main(String[]args)

This method should prompt the user for an infix expression, send that expression to the infixToPostfix method (described below), print out the postfix form, send the postfix form to evalPostfix (described below) for evaluation, then print out the integer result of evaluation.

---private static int getInfixPriority(char c) o This takes in a char (a single character) and determines the infix priority It then returns this priority

Already implemented code below

public static int getInfixPriority(char c) { switch (c) { case '(': return 4; case '^': return 3; case '*': return 2; case '/': return 2; case '+': return 1; case '-': return 1; } return 0; }

---private static int getStackPriority(char c) o This takes in a char (a single character) and determines the stack priority It then returns this priority

Already implemented code below

private static int getStackPriority(char c) {

switch (c) { case '^': return 2; case '*': return 2; case '/': return 2; case '+': return 1; case '-': return 1; } return 0; }

---private static boolean isOperand(char c) o This will return true if c is an operand (basically a single digit from 0 to 9 inclusively). It will

return false otherwise. To keep things simple, only single digit numbers are allowed in the input specified by the user. This means both the infix and the postfix notation will contain only single digit numbers. As you evaluate the expression, multi-digit numbers will naturally arise, and thats ok.

---private static int eval(char op,int a,int b) o The op character is one of the following operators:+,-,*,/,or^.These are the only operators allowed (except for parentheses which is not handled by this method).

Simply return a value of -1 if the operator is invalid. o a and b are your operands. The order goes, a op b. o This method returns the result of applying the given operator ,op,to the operands,a

and b

private static String infix To Post fix(String infix) o This method takes in an expression in infix form and produces the equivalent expression

in postfix form. Here is where your stack and queue implementations will come into play. You must implement the algorithm from the notes **Algorithm provided below**

private static int eval Postfix(String postfix) o This takes an expression in postfix form and evaluates it, returning the evaluated result.

private static StringinfixToPrefix(String infix) o This method takes in an expression in infix form and produces the equivalent expression

in prefix form.

private static int evalPrefix(String prefix) o This takes an expression in prefix form and evaluates it, returning the evaluated result.

All numbers are restricted to a single digit, no floating point numbers allowed, division symbols are handled as integer division, the final answer along with any intermediate answers are allowed to be multiple digits (i.e. it should return the mathematically correct answer, using integer division for any division)

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

GENERIC CODE FOR QUEUE

public class Queue { private List list; public Queue() { list = new List(); } public void enqueue(T value) { list.append(value); } public T dequeue() { Object container = list.getContainerAt(0); if (container != null) { T value = list.getValueFromContainer(container); list.delete(container); return value; } else { return null; } } public T peekFront() { Object container = list.getContainerAt(0); if (container != null) { T value = list.getValueFromContainer(container); return value; } else { return null; } }

GENERIC CODE FOR STACK

public class Stack { private List list;

public Stack() { list = new List(); }

public void push(T value) { list.prepend(value); }

public T pop() { Object container = list.getContainerAt(0); if (container != null) { T value = list.getValueFromContainer(container); list.delete(container); return value; } else { return null; } }

public T peekTop() { Object container = list.getContainerAt(0); if (container != null) { T value = list.getValueFromContainer(container); return value; } else { return null; } }

public boolean isEmpty() { return list.size() == 0; } }

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

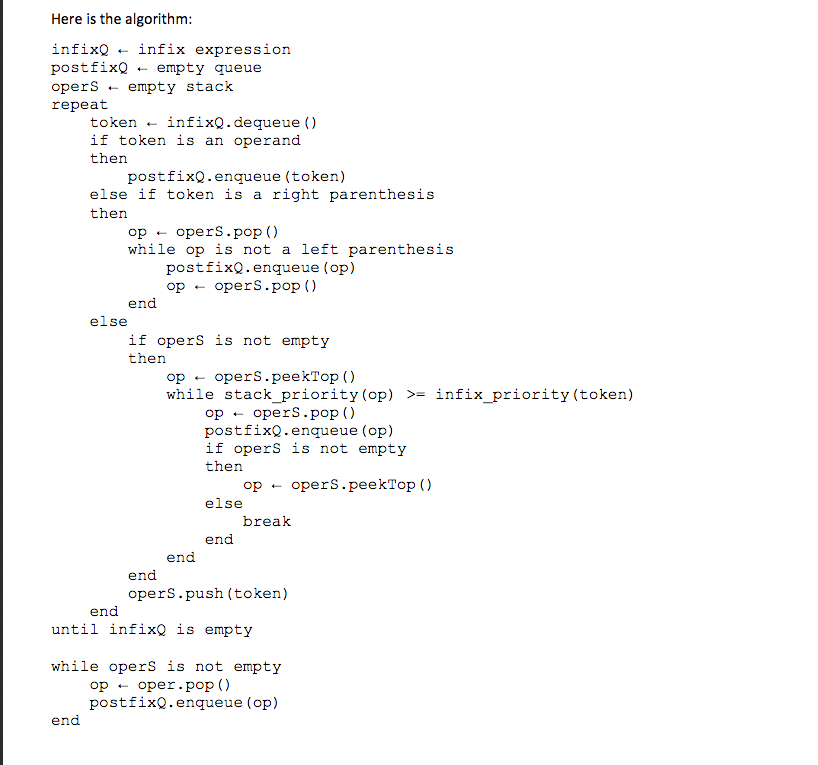
Here is the algorithm infixQ infix expression postfixQ empty queue opers empty stack repeat token infixQ.dequeue () if token is an operand then postfixQ.enqueue (token) else if token is a right parenthesis then opopers.pop () while op is not a left parenthesis postfixQ.enqueue (op) op opers.pop () end else if operS is not empty then op opers.peekTop () while stack_priority (op) >-infix priority (token) op opers. pop() postfixQ.enqueue (op) if operS is not empty then opopers.peekTop () else break end end end opers.push (token) end until infixQ is empty while operS is not empty opoper.pop () postfixQ.enqueue (op) end