To be able to use Mohr's circle to find the principal moments of inertia for an area.

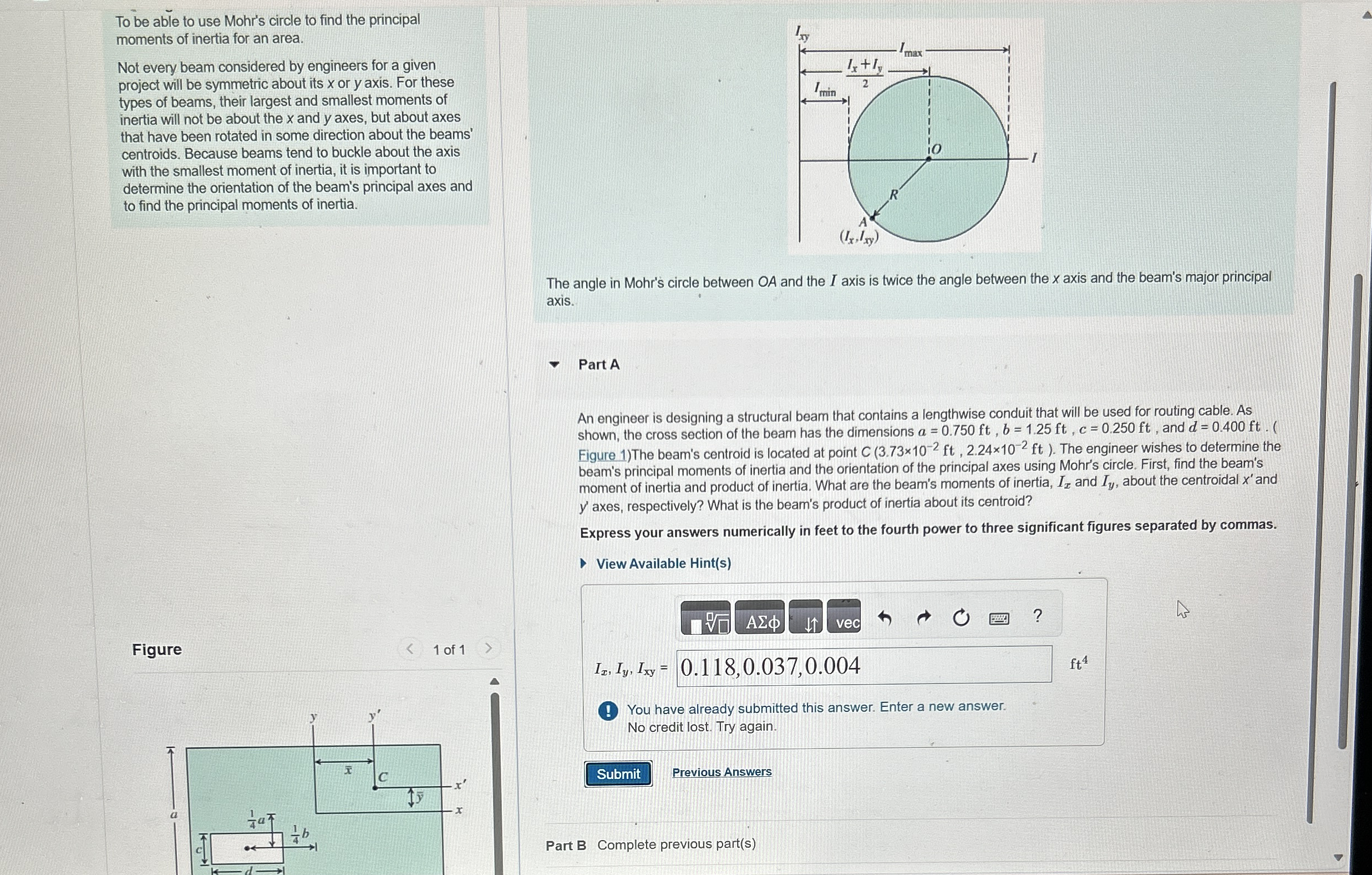
Not every beam considered by engineers for a given project will be symmetric about its $x$ or $y$ axis. For these types of beams, their largest and smallest moments of inertia will not be about the $x$ and $y$ axes, but about axes that have been rotated in some direction about the beams' centroids. Because beams tend to buckle about the axis with the smallest moment of inertia, it is important to determine the orientation of the beam's principal axes and to find the principal moments of inertia.

$$

The angle in Mohr's circle between $OA$ and the I axis is twice the angle between the $x$ axis and the beam's major principal axis.

Part A

An engineer is designing a structural beam that contains a lengthwise conduit that will be used for routing cable. As shown, the cross section of the beam has the dimensions $a=0\mathrm{.}750ft,b=1\mathrm{.}25ft,c=0\mathrm{.}250ft,$ and $d=0\mathrm{.}400ft.($ Figure $1)$ The beam's centroid is located at point $C(3\mathrm{.}73{10}^{-2}ft,2\mathrm{.}24{10}^{-2}ft).$ The engineer wishes to determine the beam's principal moments of inertia and the orientation of the principal axes using Mohr's circle. First, find the beam's moment of inertia and product of inertia. What are the beam's moments of inertia, $I_x$ and $I_y,$ about the centroidal $x\text{'}$ and $y^{\text{'}}$ axes, respectively? What is the beam's product of inertia about its centroid?

Express your answers numerically in feet to the fourth power to three significant figures separated by commas.

View Available Hint$($s$)$

$$

You have already submitted this answer. Enter a new answer. No credit lost. Try again.

$$ Previous Answers

Part B Complete previous part$($s$)$