Using Java, use this code as the starter code to complete the task

/** * This class provides the skeleton for the Pascal Triangle * assignment. */ public class PascalsTriangleBase { /** * This field controls the line spacing of the output triangle. */ protected boolean doubleSpace; /** * Simple constructor to set the value for the field. */ public PascalsTriangleBase() { doubleSpace = false; } /** * This method is the primary printing method for the triangle. * Override this method to control the spacing between values in * the output triangle. * @param n The value to be printed */ protected void printInt(int n) { System.out.print(n); } /** * This method calculates the binomial coefficient, n choose k. These * values are used to construct Pascal's Triangle. They are called * binomial coefficients because "n choose k" is the value of * the coefficient of the xk term in the expansion of * (1 + x)n. * 
For this assignment, it should use the factorial algorithm; that is * the return value should be calculated as n! / (k! (n-k)!). * @param n The power for the binomial expansion * @param k The order of the term in the binomial expansion * @return The coefficient of the kth term. */ protected int nChooseK(int n, int k) { return k; } /** * The is a special method that is used to print the first value in each * row of Pascal's triangle. The amount of "indent" for the line can be * determined by the parameter values. * @param row The number of the row being printed * @param height The height of the completed triangle */ protected void printOne(int row, int height) { printInt(1); } /** * A simple input validation routine to see if the height is ok. * @param height The requested height for the triangle * @return True if the requested height is out of range */ protected boolean heightOutOfRange(int height) { return false; } /** * The core method for this assignment. It prints out the triangle, * using the helper methods defined above. This method is marked with * the final keyword. This means that this method cannot be * overridden in a subclass. Notice that all of the helper methods * are not declared final, so they are all available for * overriding. * @param height The requested height for the triangle to be printed. */ public final void printTriangle(int height) { System.out.println("Pascal\'s Triangle of height " + height); if(heightOutOfRange(height)) { System.out.println("Height is out of range. Cannot print Pascal's triangle."); return; } System.out.println(); for(int row = 0; row  
The core of this task is to print out Pascal's triangle.
 
 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1
 
These number arranged like this give us the binomial coefficients. Let's see how this works. Take a sample binomial (a + b). Now, let's raise that binomial to successive powers.
 
(a + b)0 = 1 a0b0
 
(a + b)1 = 1 a1b0 + 1 a0b1
 
(a + b)2 = 1 a2b0 + 2 a1b1 + 1 a0b2
 
(a + b)3 = 1 a3b0 + 3 a2b1 + 3 a1b2 + 1 a0b3
 
(a + b)4 = 1 a4b0 + 4 a3b1 + 6 a2b2 + 4 a1b3 + 1 a0b4
 
If you take the coefficients, you have Pascal's triangle! Based on this, the top row of the triangle is called row 0, since that's the zero-th power of the binomial. The height of the triangle is the number of the last row. This triangle has height 4; it is made up of rows 0 - 4.
 
Now, here is another way to calculate the values for Pascal's triangle. Use this method to calculate the values for the triangle. Notice this is computationally different than the example in the text book. The book shows an example of jagged arrays. Here we're working with looping.
 
The kth value in the nth row is 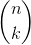 read "n choose k", 
 
where 0  
 = 
 
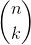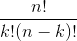
Now, n! is read "n factorial". It is calculated like this: n!=1x2x3...(n-1). By definition, 0! = 1
 
The coding task is to create a subclass that overrides the protected methods of PascalsTriangleBase. Name the subclass PascalsTriangle. This will complete the functionality to print the triangle. Notice the "key" method is printTriangle, which takes an int parameter, the height of the triangle. You cannot override this function. (See the keyword final. It prevents overriding this method. That's a little preview of next week's topics.)
 
public final void printTriangle(int height)
 
The method shall accept height values between 0 and 10, inclusive. (We will alter the upper limit for the challenge version.) If the parameter value is out of range, print out an error message and exit the method.
 
If we limit the height to 10, all of the entries in Pascal's triangle will be less than 300. This makes pretty printing easier, since the values will all be 3 digits or less. Notice the printTriangle method prints out a label above the triangle and a blank line below it.
 
In your subclass, add a main method that calls the printTriangle method several times. Here is a simple sample main. This method does not meet the requirements for main, described below.
 
public static void main(String[] args) { PascalsTriangle pascal = new PascalsTriangle(); pascal.printTriangle(4); pascal.printTriangle(1); pascal.printTriangle(3); }
 
This would generate an output similar to the following:
 
Pascal's Triangle with height 4: 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 Pascal's Triangle with height 1: 1 1 1 Pascal's Triangle with height 3: 1 1 1 1 2 1 1 3 3 1
 
The main Method
 
The core of this assignment is a method that prints out the Pascal's triangle of the height given in the parameter.
 
For this assignment, the application method (main) shall call the printTriangle method for each of the four values of your test cases. See the LA write-up for the instructions for determining your test case values. To check your input validation, call printTriangle a fifth time, passing the value -1. This should generate the error message. The program should end normally.
 
Check the output against what you submitted for the lab.
 
Notes
 
Now, the point of this assignment is to work with loops. So, the values in the triangle need to be calculated "on the fly". If you submit a program with hard-coded values for the triangle, you will receive a very bad score. This also applies to the "sum of the two upper neighbors" algorithm that is shown in the text book. Use the factorial algorithm shown above.
 
Notice input validation in supported. If the input to printTriangle is out of range, an error message will be printed instead of the triangle.
 
You may have it helpful to create some "helper" functions. These helper functions should be private.
 
There needs to be :
 
1. Pretty printing
 
2. Command-line arguments
 
For pretty printing, arrange the triangle as described above:
 
the last line has it's first "1" in the first column
 
the one's column of alternating rows align vertically
 
the one's columns within any given row are spaced evenly
 
the rows of value alternate with blank rows
 
It shall also look at the command-line arguments, the args parameter of main. Depending on the value of the parameter, the output triangles will be different.
 
If there are no command-line arguments, print out the triangles for your four test cases and for -1, as instructed above.
 
If the command-line argument is the word "all", use a loop to print out the triangles for 0 - 10, inclusive. That's eleven triangles.
 
If there are command-line arguments, but it is not the single word "all", assume that those arguments are numerical values. Convert them to int values using Integer.parseInt, and print out the corresponding triangles.
 
Then
 
Increase the upper limit for height to 15. This will cause several following changes:
 
The maximum value you need to output is 6,435. So the horizontal space within each line must increase.
 
The factorial calculation, n! / ( k! (n-k)! ), obviously includes the value n!. However, 13! is 6,227,020,800 which is greater than the largest int value, which is 2,147,483,647. (12! is still a valid intvalue.)
 
Update the nChooseK method to use two different version of the algorithm. If the value of n is 12 or less, use the standard algorithm with the three factorial values. If the value of n is greater than 12, modify the algorithm so that the intermediate values do not exceed the maximum int value. (No, the solution is not to use long, float, or double. And, yes, you still have to use this factorial version of calculation.) Hint: Think "cancelling".