Weak law of large

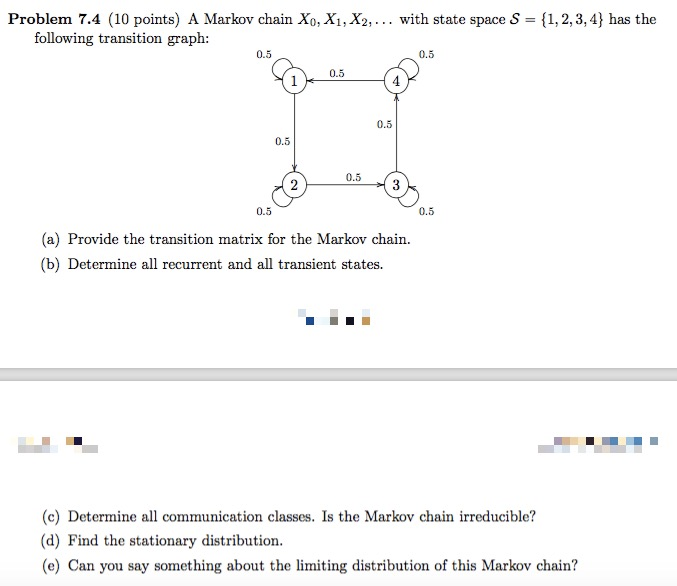
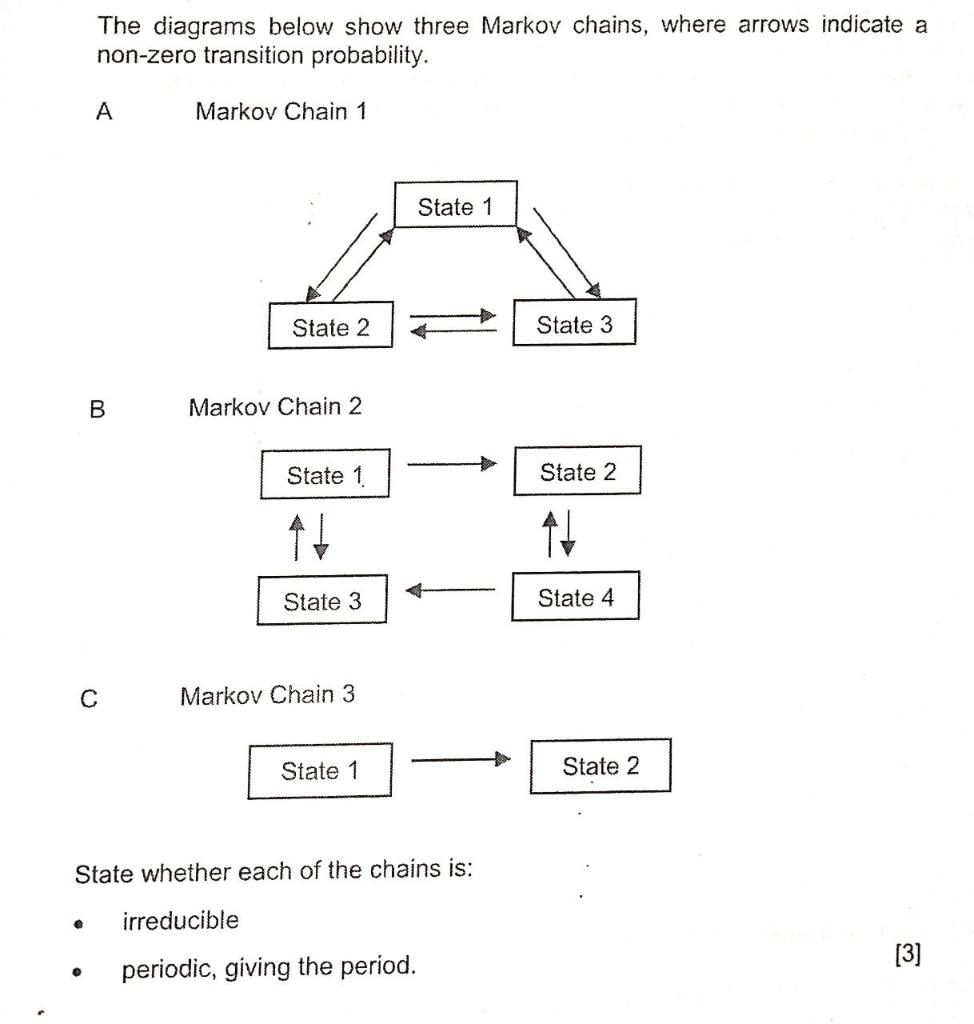
Problem 7.4 (10 points) A Markov chain Xo, X1, X2, ... with state space S = {1, 2,3, 4) has the following transition graph: 0.5 0.5 0.5 1 0.5 0.5 0.5 2 0.5 0.5 (a) Provide the transition matrix for the Markov chain. (b) Determine all recurrent and all transient states. (c) Determine all communication classes. Is the Markov chain irreducible? (d) Find the stationary distribution. (e) Can you say something about the limiting distribution of this Markov chain?The diagrams below show three Markov chains, where arrows indicate a non-zero transition probability. A Markov Chain 1 State 1 State 2 State 3 B Markov Chain 2 State 1 State 2 State 3 State 4 C Markov Chain 3 State 1 State 2 State whether each of the chains is: e irreducible . periodic, giving the period. [3]1. (a) Explain what is meant by the transition probability matrix of a homogeneous Markov chain. [5 marks] (b) Explain what is meant by the stationary distribution of a Markov chain? [5 marks] (c) A Markov chain has transition probability matrix, A, with entries Ouj; and stationary distribution . Write down an expression for the entries of the reverse Markov chain. [5 marks (d) Consider the following transition probability matrix of a homogo- neous Markov chain, with three states i,j and k (the TPM is in that order). If the stationary vector of the chain is (1/9, 2/9, 2/3), determine whether the Markov chain is reversible. 1 /0.2 0.2 0.6 0.1 0.6 0.3 4 \\0.1 0.1 0.8 [5 marks] (e) Let X1, X2, Xa be a sequence of random variables resulting from the above Markov chain. If X1 = i and Xs = j what is the probability that X2 = k? [5 marks]SECTION 5.2. The Weak Law of Large Numbers Problem 4. In order to estimate f, the true fraction of smokers in a large population. Alvin selects n people at random. His estimator Mn is obtained by dividing Sn, the number of smokers in his sample, by n, i.e., Mn = Sn. Alvin chooses the sample size n to be the smallest possible number for which the Chebyshev inequality yields a guarantee that P(IMn - 1 Z E) 56, where e and o are some prespecified tolerances. Determine how the value of n recom- mended by the Chebyshev inequality changes in the following cases. (a) The value of e is reduced to half its original value. (b) The probability o is reduced to half its original value