When an interrupt occurs, control must be transferred from the currently executing program to a subroutine that handles the activity required to service the interrupt. For each interrupt, a "context switch" is said to occur. In addition to transferring control, a context switch includes the saving and restoration of any required registers. Assume that it takes 1000 clock cycles to perform each context switch when an I/O device triggers an interrupt. The interrupt handler subroutine takes an additional 8,000 cycles to service the device request. Once the device has been serviced, another 1000 cycles are required to perform the context switch needed to return from the interrupt handler back to the program that was running. The processor's clock rate is 2 GHz.
a) (5) What is the maximum number of requests per second that a device can generate if the system must complete every activity associated with each interrupt, including the context switches, before the next interrupt occurs?
b) (5) The registers used in managing exceptions and interrupts on our MIPS processor are described in the sub-module "2.2 Interrupt Driven Input/Output" as well as in section A.7 of the textbook. Write down a short sequence of MIPS true-op assembly language instructions that reads the current exception code and places just the code right justified into CPU register $t0. No CPU registers other than $t0 should be modified or saved by the instruction sequence.
c) (5) Suppose that interrupt driven I/O is used and a device issues 10000 evenly spaced requests per second to transfer 1 byte per request. If each instruction takes one clock cycle, how many instructions, other than those related to I/O, can the CPU perform each second?
d) (5) Suppose that instead of interrupt driven I/O, DMA is used to transfer a 10000-byte data block each second. If each instruction takes one clock cycle, how many instructions, other than those required for I/O, can the CPU perform each second?
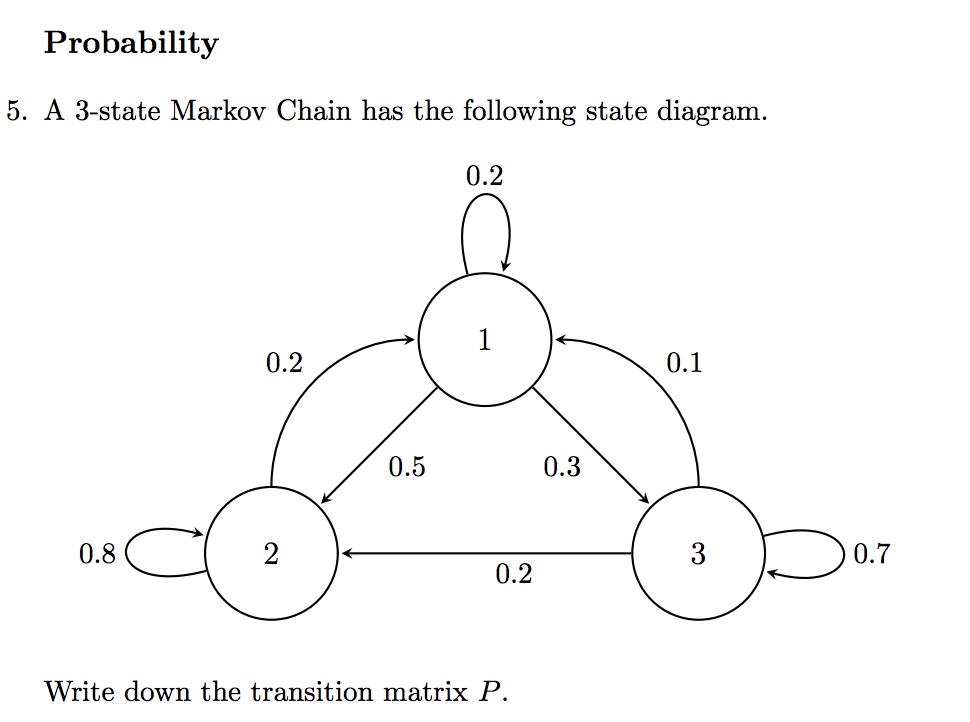
Name For the following word problems state if the problem requires using the Central Limit theorem or if does Not require using the Central limit theorem Circle the correct choice: 1. What is the probability of randomly selecting an adult with an IQ score less than 75? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 2. If 30 cell phones are randomly selected what is the probability the cell phones will last an average of more than 23.8 months? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 3. In general Marine platoons are around 50 strong, if a sample of a given platoon is taken from a population of Marines with a mean weight of 200 pounds and with standard deviation o = 10. What is the probability that the sample mean weight will be less than 196 pounds? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 4. The mean age of baseball players is 27 years. Assuming the age of baseball players are normally distributed and that the average size of a baseball team is 25 players, what is the probability a baseball player is older than 30 years if the player is randomly selected. A. Requires the Central limit theorem. B. Does not require the central limit theorem. 5. Suppose that you have a sample of 81 students from a population with mean u = 500 and with standard deviation o = 108. What is the probability that the sample mean will be greater than 483. A. Requires the Central limit theorem. B. Does not require the central limit theorem. Page 1 of 1For the following word problems state if the problem requires using the Central Limit theorem or if does Not require using the Central limit theorem Circle the correct choice: 1. What is the probability of randomly selecting an adult with an IQ score less than 75? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 2. If 30 cell phones are randomly selected what is the probability the cell phones will last an average of more than 23.8 months? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 3. In general Marine platoons are around 50 strong, if a sample of a given platoon is taken from a populati of Marines with a mean weight of 200 pounds and with standard deviation o = 10. What is the probabil that the sample mean weight will be less than 196 pounds? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 4. The mean age of baseball players is 27 years. Assuming the age of baseball players are normally distributed and that the average size of a baseball team is 25 players, what is the probability a basebal player is older than 30 years if the player is randomly selected. A. Requires the Central limit theorem. B. Does not require the central limit theorem. 5. Suppose that you have a sample of 81 students from a population with mean u = 500 and with standard deviation o = 108. What is the probability that the sample mean will be greater than 483. A. Requires the Central limit theorem. B. Does not require the central limit theorem.Problem 1: A Central Limit Theorem Simulation Here we will perform a Central Limit Theorem simulation similar to the ones done in class. That is: . Pick a distribution (that was not presented in class) . Justify that the distribution will abide by the central limit theorem . Find a parameter set and value for / where we can see that the central limit theorem clearly applies . Find a parameter set and value for / where we can see that the central limit theorem does not apply . Code must be submitted (preferably in R, but MATLAB, Python, ForTran, and C++ will also be accepted).Probability 5. A 3-state Markov Chain has the following state diagram. 0.2 0.2 0.1 0.5 0.3 0.8 N 0.7 0.2 Write down the transition matrix P