In Figure 11.5, we show three combinations of main effects and interactions for a 2 × 2 factorial design. Using the same 2 × 2 structure, with factor A defining the rows and factor B defining the columns, create a set of means that produce each of the following patterns:
a. A main effect for factors A and B, but no interaction.
b. A main effect for factor A and an interaction, but no main effect for factor B.
c. A main effect for both factors and an interaction.

Figure 11.5

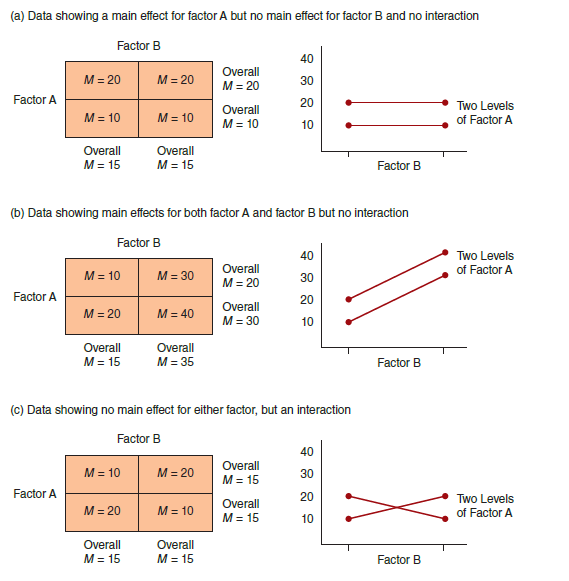
(a) Data showing a main effect for factor A but no main effect for factor B and no interaction Factor B 40 Overall M = 20 M = 20 30 M = 20 Factor A 20 Two Levels of Factor A Overall M = 10 M = 10 M = 10 10 Overall Overall M = 15 M = 15 Factor B (b) Data showing main effects for both factor A and factor B but no interaction Factor B 40 Two Levels of Factor A Overall M = 20 M = 10 M = 30 30 Factor A 20 Overall M = 30 M = 20 M = 40 10 Overall Overall M = 15 M = 35 Factor B (c) Data showing no main effect for either factor, but an interaction Factor B 40 Overall M = 15 M = 20 M = 10 30 Factor A 20 Two Levels Overall M = 20 M = 10 of Factor A M = 15 10 Overall Overall M = 15 M = 15 Factor B