The SuSchriefferHeeger (SSH) linear chain model also has two orbitals per unit cell, but envisions these as
Question:
The Su–Schrieffer–Heeger (SSH) linear chain model also has two orbitals per unit cell, but envisions these as two different atoms with only one relevant atomic orbital on each. Each atom couples differently to its neighbors on the right and on the left, with coupling terms v and w, respectively, giving the Hamiltonian
for periodic boundary conditions. For free ends, the same matrix is used but with the w terms in the upper right and lower left corners dropped.
(a) Show that the SSH Hamiltonian is equivalent to (1.12.5) for the special case Uss = Upp = Usp. To do this, show that a simple transformation of the basis converts the SSH matrix into (1.12.5). Consider what basis transformation will make one 2× 2 block on the diagonal of (1.12.6) into the 2 × 2 diagonalized block at the same location in the matrix (1.12.5).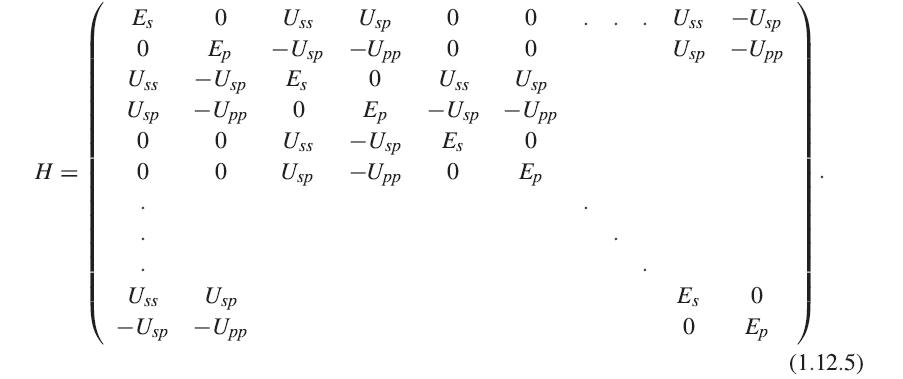
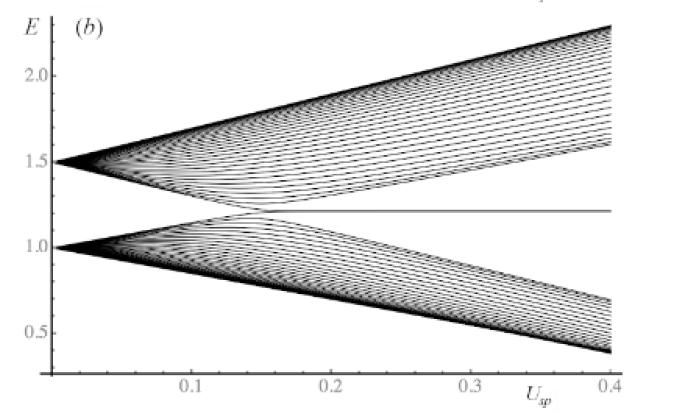
(b) Show, for as many atoms as your computer resources can handle, that the SSH model gives qualitatively the same behavior as seen in Figure 1.41.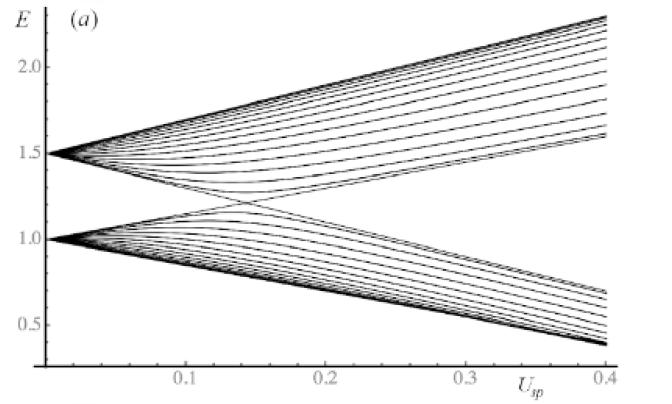
Step by Step Answer:
a The block V 0 1 0 looks like the Pauli matrix or which can be transformed to oz by a 90 rotation a...View the full answer
